参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすく、どの参考書よりも細かく解説をしていきます。
2022千葉大大問1
問題


これは確率の問題ね。結構難しそう。

この問題のポイントは次の3つだよ
この問題で大事なことは次の3つ
- 取り出した球は袋に戻さないので反復試行ではない
- 円形を進む問題と数直線を進む問題の違い
- 試行が3回で黒は3連続取り出せるが白は2回しか取り出せない
反復試行ではない
戻さないということは全事象(確率の分母が減っていく)こと。
最初に6個あったのが5個→4個と減っていくことに注意
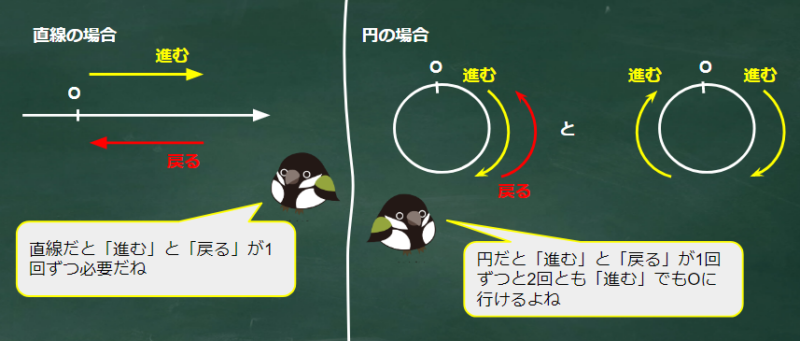
円形に進む
数直線で原点を出発する問題はよく見かけます。
これは進む動作と戻る動作がないと原点に戻ってはこれません。
この問題は円形を進むので同じ方向にに進み続けてもA1に戻ってこれることに注意が必要。
試行回数
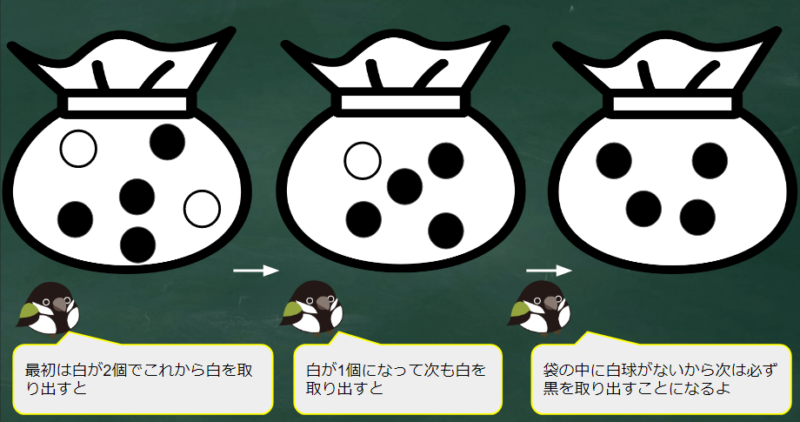
試行回数は全部で3回。
袋に戻さないので2回連続白を取り出すと3回目に袋の中には黒しか残っていない。
解説
(1) の解説


①と②は同じような事をやってるし,答えも同じだからまとめてやったらどう?

確かに結果的には同じだけど手抜きの解答はミスにつながりやすいから一つずつ丁寧に計算したほうがいいよ。
ここまでは考えつくけど次を忘れてない?

2回とも同じ色で2回とも6の目が出ると円を1周してA1に戻れるよ。

確率の問題はしっかり数えたつもりでも抜け漏れがあることが多いです。問題をしっかり把握する練習をしましょう。
(2) の解説
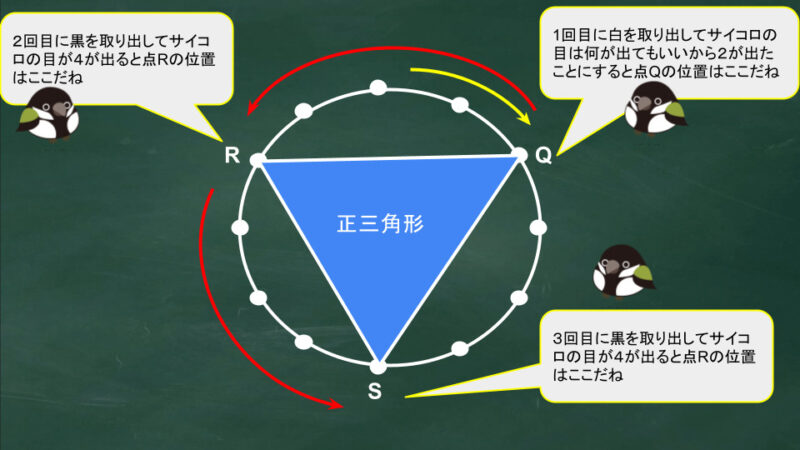
3点を結んで正三角形ができるためには次の条件を満たすといいよ。
- 1回目の操作で移動した点Qはどこにあってもいい
- 3点P,Q,Rは等間隔になるのでそれぞれの点同士が4つ隣にある(間に点が3つと考えてもいいよ)
- 2の条件を満たすには2,3回目同じ方向に回らなければならない

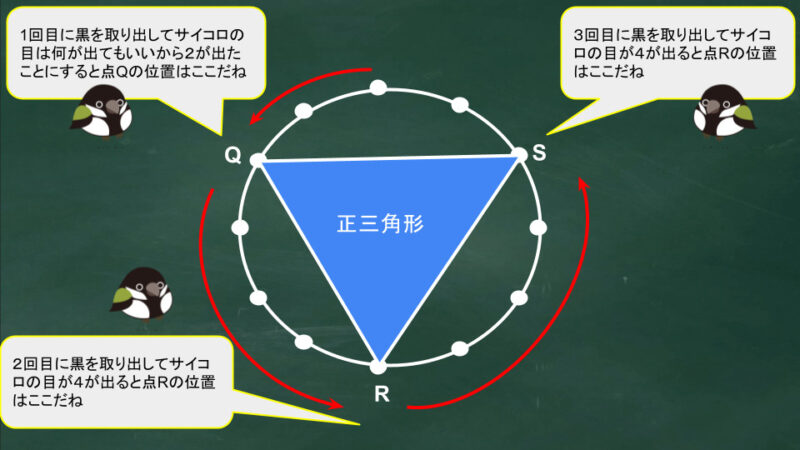
次も同じように考えるんだけど袋の中に入っている白球と黒球の数が違うから同じ答えにはならないよ

袋に入っている白球は2個しかないので3回とも白球を引くことはない。

だからあとは3回とも黒球を引く場合を考えればいいのね。

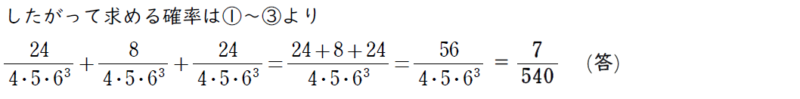
終わりに

確率を勉強するときは図を書いたり、表を作ったりするといいよ。

問題文だけで考えると見落としてしまう試行があったりするからね。
今回の解説では「同様にして~」とか「対称性を利用して~」とかを使わずに一つ一つ丁寧に計算する解答を紹介しました。
確率は特にミスの多い分野なので演習のときは特に丁寧な解答作りを心掛けてね。
確率の全事象(分数の分母)は途中で約分や計算をせず,最後にまとめた後に計算するとミスが少なくなるよ。










コメント