参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022神戸大大問4(理系)
問題

問題文を見ると双曲線の方程式なので数学Ⅲの分野かなと思われるが、内容は2次関数の「解をもつための条件」が中心となっている。
注意しないといけない点は「分数関数」や「無理関数」の定義域と値域の条件。
他にも「解と係数の関係」や「軌跡」の内容も入っているので幅広い学習が必要となる。
この問題は、同じ神戸大学の文系の大問2の問題と類似しているので解き比べてみよう。
解説
直線の方程式に文字 a が入っているので場合分けが必要になる。
前半で求めたものが後半に使われるパターンなので答えをしっかり合わせることが完答へとつながる。
(1) の解説
まずは双曲線と直線を連立して2次方程式をつくる。

① と ② が異なる2点 P,Q で交わるためには ③ が異なる2つの実数解をもてばよい。
③ の最大次数 x2 の係数が 0 になると1次式になるので解を2つもつことができない。
まずはその場合分けを行おう。

(2) の解説
双曲線と直線の2つの交点P,Qの座標を直接求めるのは大変なので「解と係数の関係」を用いる。
ここでも分母に文字が入るときは注意が必要になる。

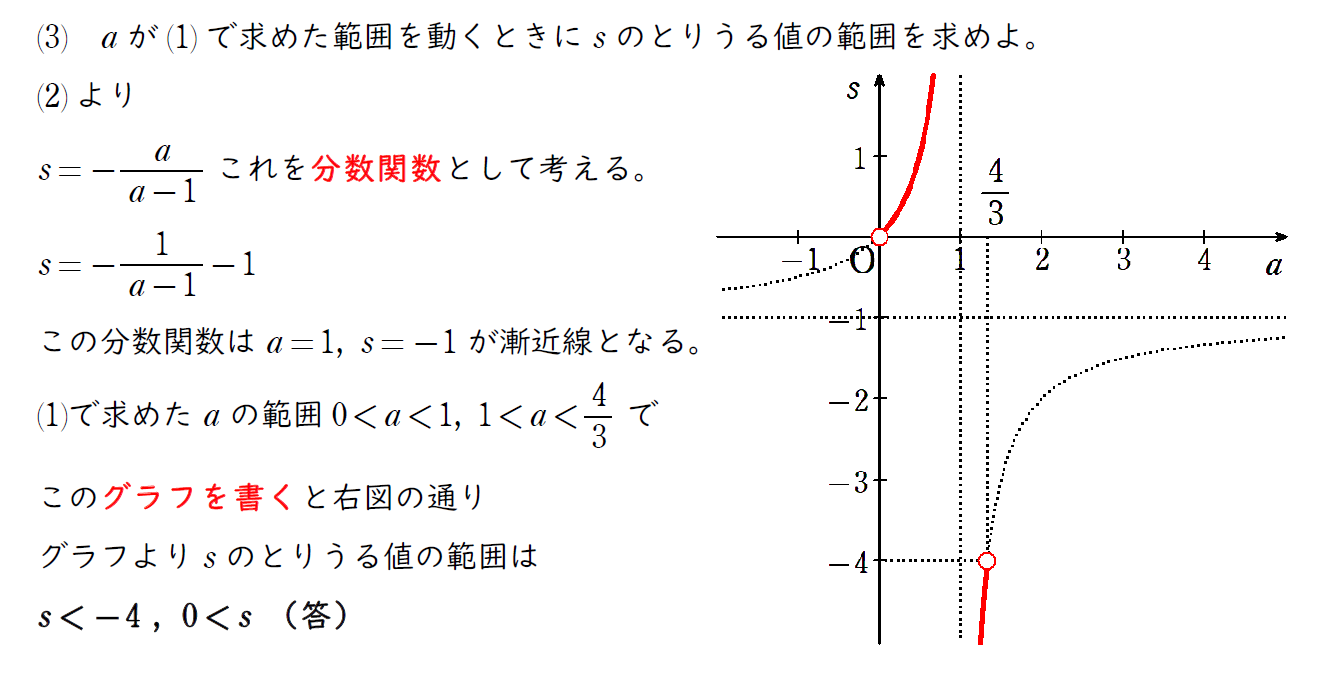
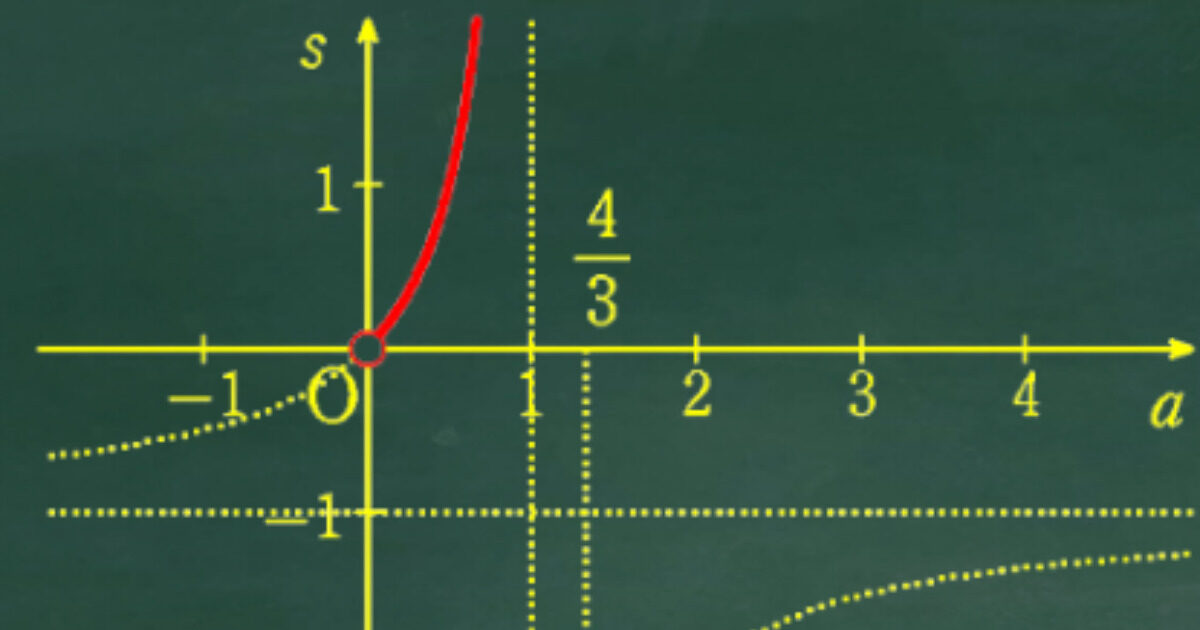
(3) の解説
s の式が「分数関数」の形をしているので範囲を求めるにはグラフを利用するとよい。
(1) の a の範囲も関係してくることを忘れずに。
(4) の解説
これは軌跡の問題だが (3) まで丁寧に誘導してくれているので、あとは a を消去するだけ。
解答の最後にある通り、無理数の取り扱いには注意が必要。

解答はここで終了していいのだが、A の s+1 の部分をルートの中に入れる場合には注意が必要。
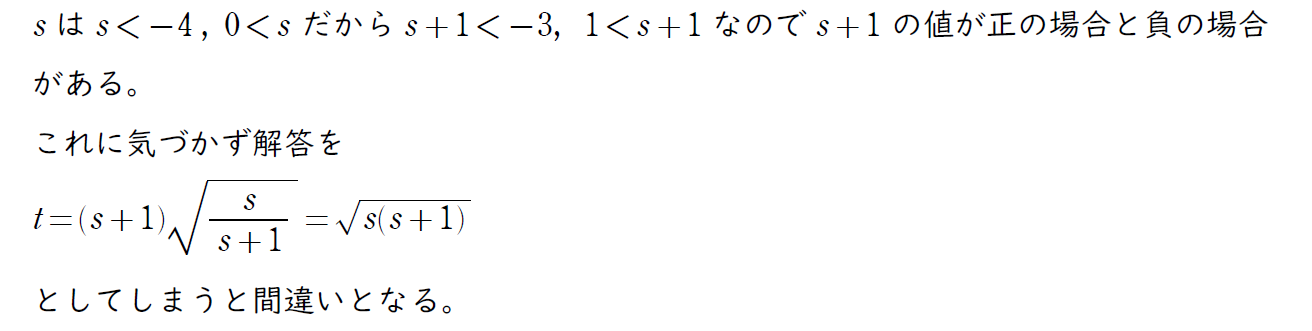
この形の方がすっきり見えるので、ここまで変形してしまう受験生も多いかもしれない。
どうしてもここまで変形したい人は次のように場合分けをしなければいけない。
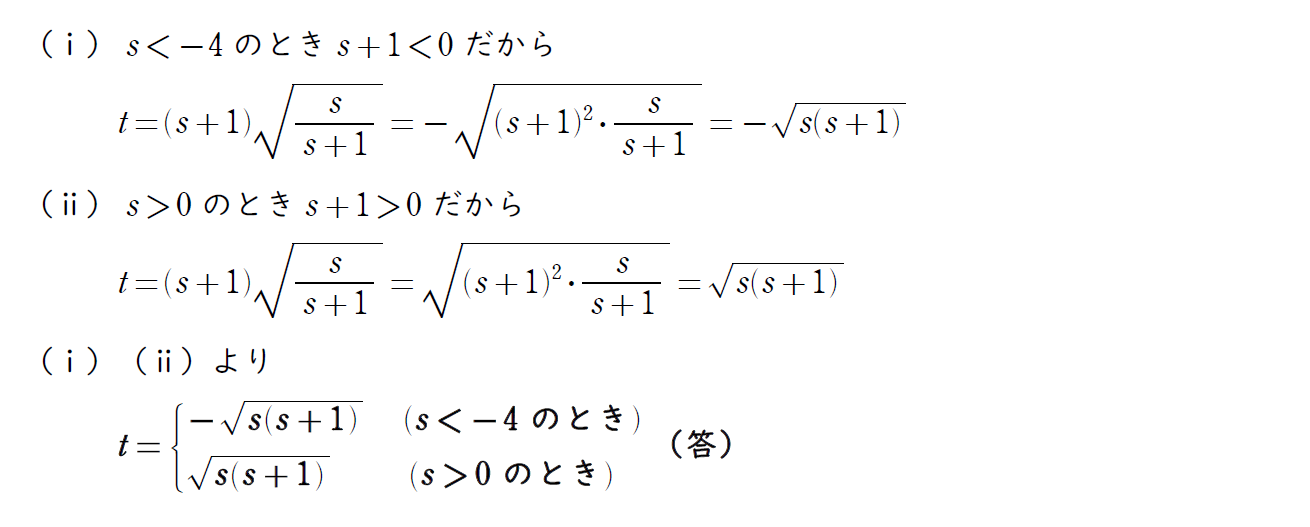
終わりに
いろんな分野からまんべんなく出題されている問題。
教科書の基本事項をしっかり押さえておけば完答できる。
(4) は無理に変形をすると、気づかないうちに間違っている可能性があるので注意が必要となる。









コメント