参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022千葉大大問9
問題


この問題は微分の問題ね。

その通り!関数の増減は微分係数で調べるんだったね。
この問題で大事なことは次の3つ
- 第1次導関数は曲線の接線の傾きを意味するので関数の増減が調べられる
- 関数の中にx以外の文字が入っている場合は文字定数を分離させて考える
- 周期関数(三角関数)のグラフを考えるときは定義域を0から2πに絞る
解説

(1) はrに1を代入するので微分をしたらあとは符号を考えるだけね。(2) はrが残ったままだけどどうするの?

そこがポイントになるね。解法は数学Ⅱでも出てくる「定数分離」を使うんだけど、方針が立っても計算がとても複雑で大変だよ。
(1) の解説
この問題は関数f(x)が常に増加することを示すのでf'(x)>0がいえるといいんだね。
(2) のことも考えてr=1を代入するのは微分してからがいいね

A-Bの符号の判断の仕方は次の通り ↓


(2) の解説

(1) は (2) の例を挙げてくれているのね。

(2)の難しいところは変化する文字定数rが入っていることだね。

r=1のときf(x)は常に増加することが分かったんだけど、このrの値が変化するときはどうするの?

(2)ではその変化するrを切り離して考える「文字定数の分離」を使った解法になるよ。
まずは文字定数分離の考え方を例を挙げて紹介するね。
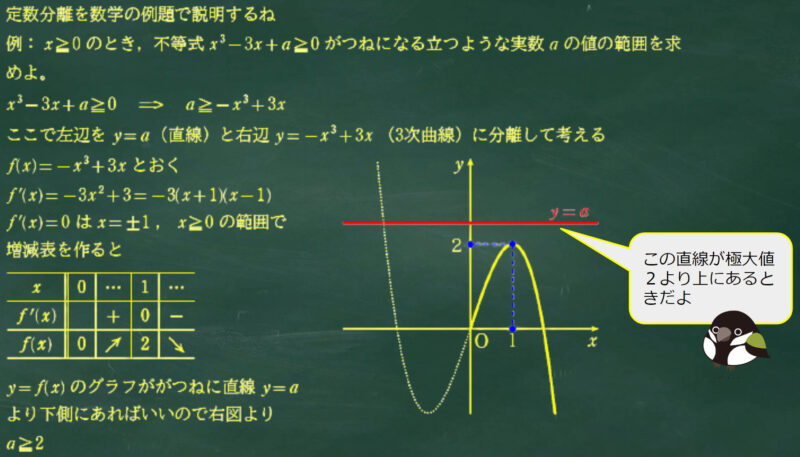
ここからが (2) の解説だよ。

この式を難しくしているのはrの存在だね。上で説明した文字定数分離を次の方法でやってみたが行き詰まった。

そこでrの分離の仕方を次のように工夫して進めてみよう。

これで定数rがなんとか分離できたね。
次はこの右辺の式のグラフを書いていこう。
三角関数のグラフを考えるときに定義域(xの範囲)に制限がない場合、一般角を使うことになる。
この問題みたいに周期関数の確認が取れたらグラフは 0≦x≦2π の範囲で考えた方が楽だよ。

三角関数の問題では定番なんだけど2倍角とかの公式を使って式をsinx、cosxのどちらかに統一するといいよ。
ここではsinxに統一するけど、もしかしたらcosxに統一した方がいいのかも。
これは実際にやってみないとわからないね。これも行き詰まったら戻ってやり直そう。

三角関数の増減表はただでさえ難しいのに角度が求められないこの問題だと、単位円を使って増減を調べるしかないよ。

ここからが解答だよ。増減表を作ってみよう
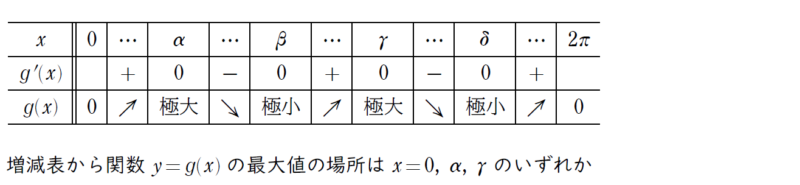
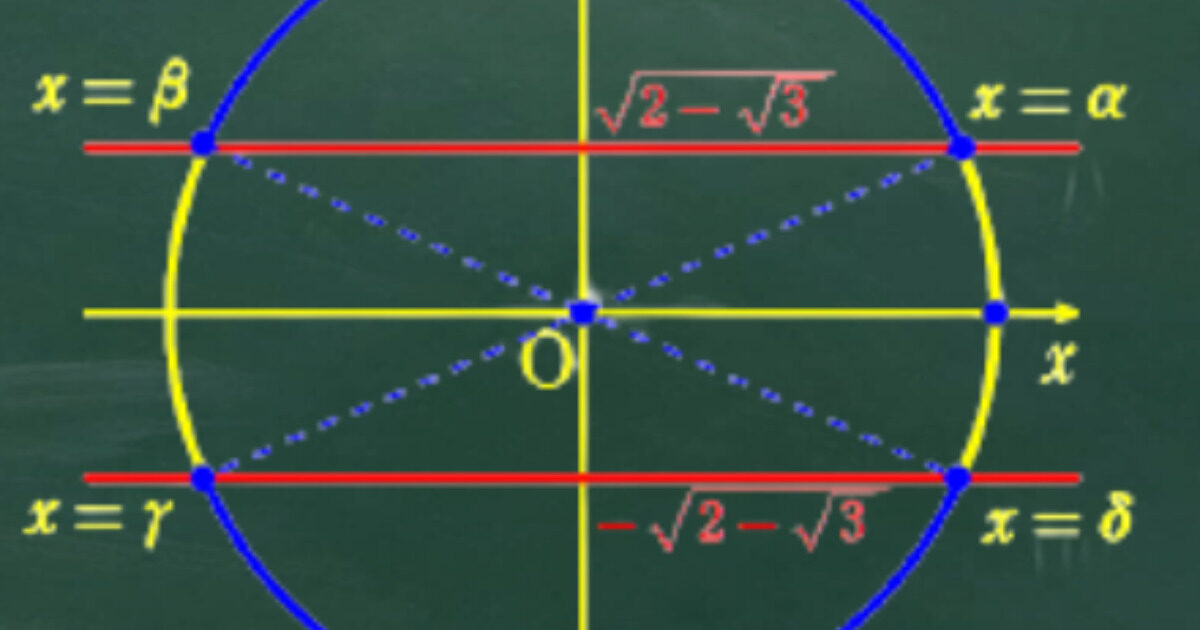
増減表ができたので0≦x≦2nπの範囲では最大値の場所が断定できるよね。これと③の左辺の2/rの比較をしたらこの問題は解決だよ。

*この問題はかなり難易度が高いのでこのブログのコンセプトである「誰にでもわかりやすく解説」の実行ができてないかもしれません。
終わりに
国立大学の問題は教科書の知識を超えない範囲で出題されます。
つまり教科書のどこかにある知識を使ってそれを組み合わせ、繁雑な計算をこなせるような計算力を付けることが大切だよ。
難問・奇問に取り組むよりも教科書をしっかり解きなおすことが合格への近道だね。







コメント