参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022千葉大大問8
問題


これは数学Ⅲの積分の問題ね

いつもと違う生徒だな

とりこは数学Ⅲがわからないというので私が代わりに来ました。つぶこです。

つぶこさんよろしく。数学Ⅲの問題は難しいから頑張ってね
この問題で大事なことは次の2つ
- 積分を利用した不等式の考え方
- 極限の問題におけるはさみうちの原理
解説
まず最初に定積分を利用した不等式の考え方とはさみうちの原理を説明するね
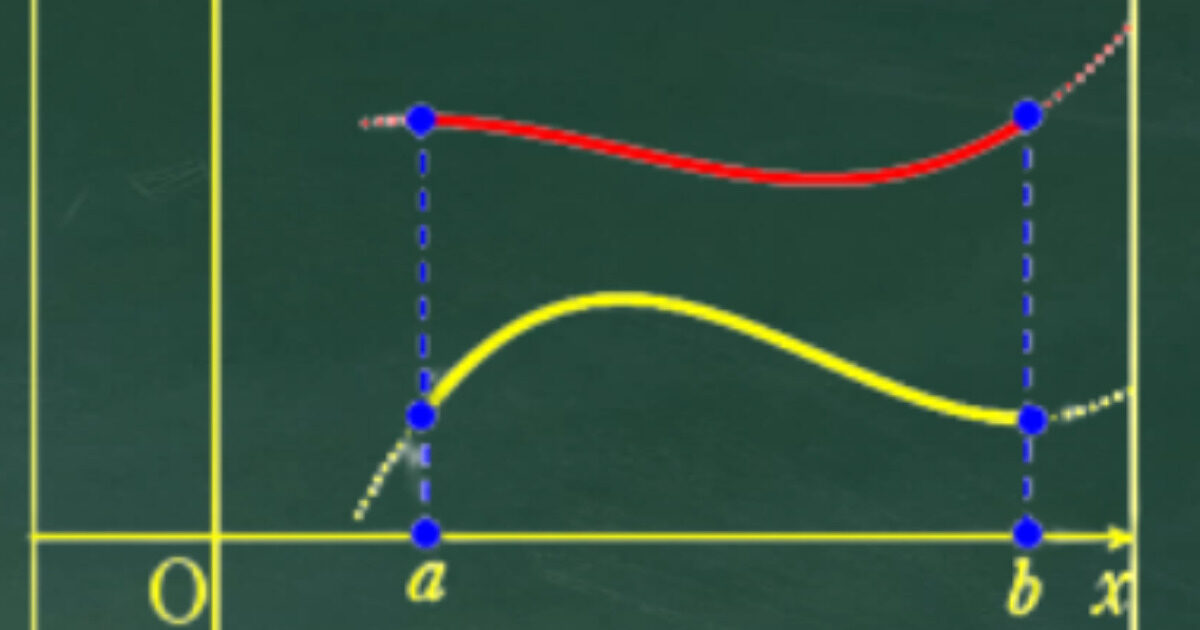
定積分を利用した不等式
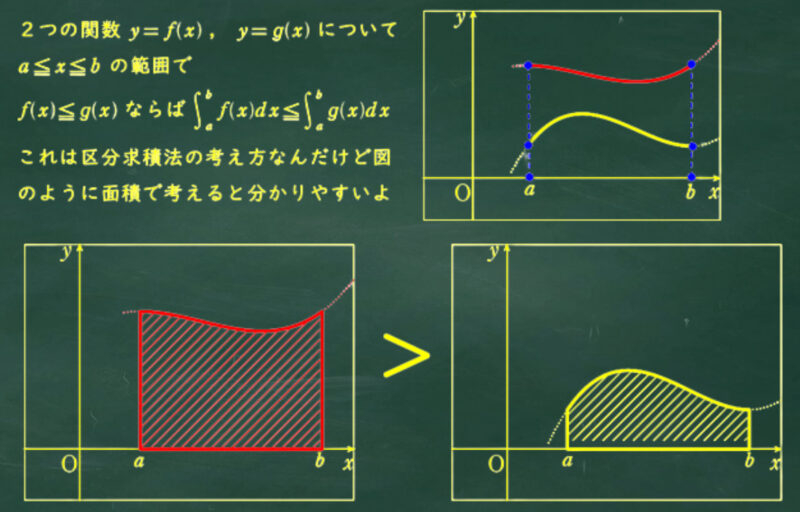
はさみうちの原理

(1) の解説

定積分を利用して不等式を作ることはわかったんだけど、何もヒントがない状態から式を立てるのは難しいわ

それがこの問題のポイントなんだ。次の流れを見て式を作ってみてね
解答の流れ
- 不等式は定積分範囲から作る
- 不等式の中央の項を積分の中身の形に変形する
- 各項をxについて積分する


1,2の解答ができたらあとは3の積分計算なんだけど、計算するときは各項を次のようにばらして行うといいよ。

(2) の解説

この問題は(1) を使えば「はさみうちの原理」ですぐに解けるね

すごい!なかなか優秀だね。その考え方で早速解いてみよう。

(3) の解説

(2)はあっさり解けたけど、(3)は似たような問題なのに解けないわ

解けない原因を考えてみよう
この問題のポイントは m→∞ の極限を考えるんだけど A(m,n) の中にある (m+1) の部分が邪魔してるんだ。これをうまく消すことを考えた変形が必要だね。

部分積分法をここで説明しておくね
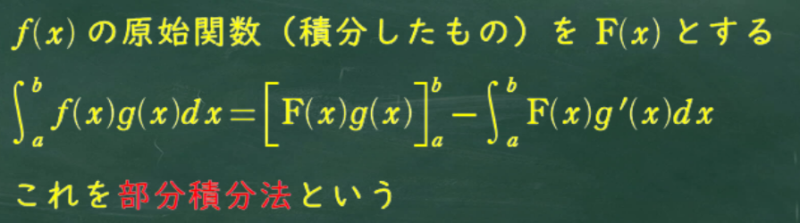
解答の続き
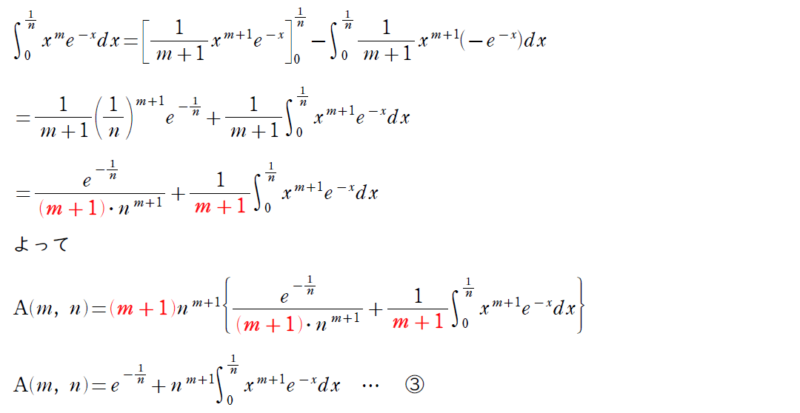

m+1の消し方はなかなか思いつかないわ。結果を見て初めて消えることが分かったもの

確かに思いつくのは難しいね。解答の見通しを立てる練習をいっぱいやるしかないよ。
ここから先は (1) と同じはさみうちの原理で解答を作っていくよ。

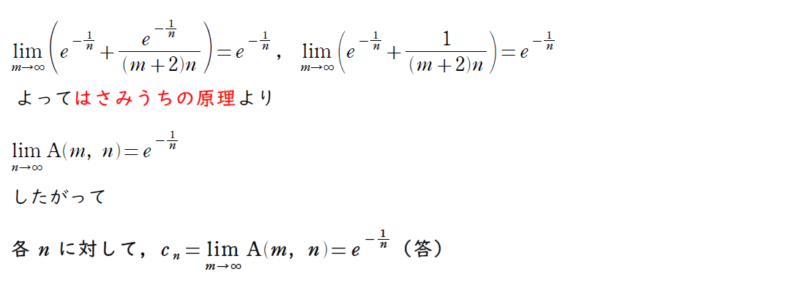
終わりに
区分求積法の考え方を応用した「定積分を利用した不等式」は多くの大学で証明問題に使われているよ。
積分マーク(インテグラル)の入った不等式はほとんどがこの証明方法だといってもいいかな。
解答の中でも取り上げた「不等式をどこから作るのか?」が一番難しいポイントだったね。
とにかく多くの問題に触れることがこの証明問題の攻略につながるので、いろんな大学の過去問から探してどんどんチャレンジしてみよう!








コメント