参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022大阪公立大大問3(理系)
問題


前半は整数の問題だけど後半は複素数の問題ね

複素数平面はいろんな分野との融合問題を見かけるので練習が必要だね
この問題で大事なことは次の2つ
- 問題が誘導になっていることに気づく
- 証明問題の方針の立て方をしっかり考える
解説

(1)(2)は何とかなりそうだけど(3)(4)は見るからに難しそうね

(3)(4)は「示せ」の問題なので解くための方針をしっかり考える必要があるよ
(1)の解説

これは1次不定方程式の特殊解を求める問題ね

ユークリッドの互除法を使ってもいいけど計算が大変になるので、数字が小さいときは使わずに見つけたいよね
この問題は次の解答のように整式の「割る数、商、余り」の関係を考えると求めやすいよ。

(2)の解説

「存在しないことを示せ」は難しくない?

ここは左辺と右辺の「矛盾」を説明する証明だよ。
1次の不定方程式px+qy=1は「pとqが互いに素」でないと成立しないんだよ

(3)の解説

ここから複素数の問題ね。

ここで使う「ド・モアブルの定理」を復習しておこう。


この証明の解法の根拠になる部分を説明するね。


(4)の解説

これも証明問題ね。

「pとqは互いに素」を示すには背理法を使うよ。

ここの計算では複素数の積を使うよ。
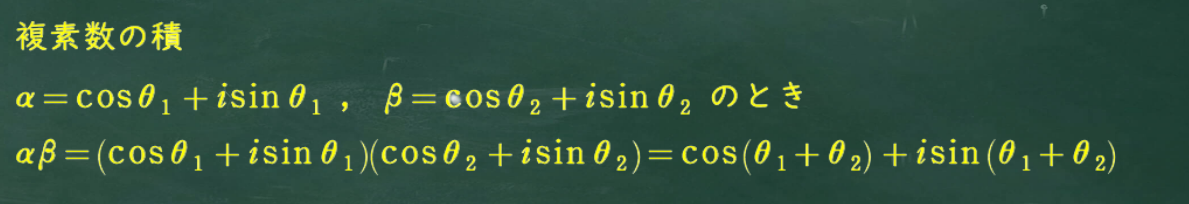
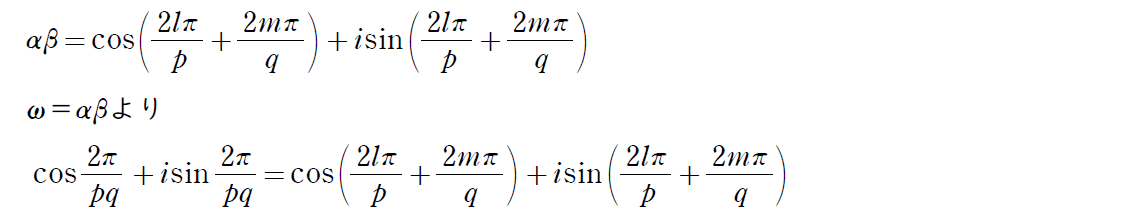
三角関数の方程式は少し難しい部分があるよ。




終わりに
国公立の個別試験でよく見かけるのが「前半の誘導を利用した解法」だね。
前半部分は基本がしっかりしていれば得点源になる部分で、さらに後半のヒントにもなっているので間違えないようにしっかり解く練習をしておきたいところだね。
整数の証明問題は「背理法」を用いて矛盾することをいうパターンが多いのでしっかり練習しておこう。










コメント