【2023】北海道大学入試問題数学大問１(理系）をとことんわかりやすく動画を使わずに解説します

参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか？

YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。

この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。

2023北海道大大問１（理系）

問題

複素数平面の問題。

(1) で証明したことを使って最後は極限値を求める。

解説

(1) の解説

この証明には数学的帰納法を用いる。

数ある証明方法の中でも整数や自然数の命題に対しては、数学的帰納法を使うケースが多い。

証明の中で出てくる式から漸化式を作り、一般項を求める。

ここからは数列の漸化式の問題。

初項もしっかり求めておこう。

(2) の解説

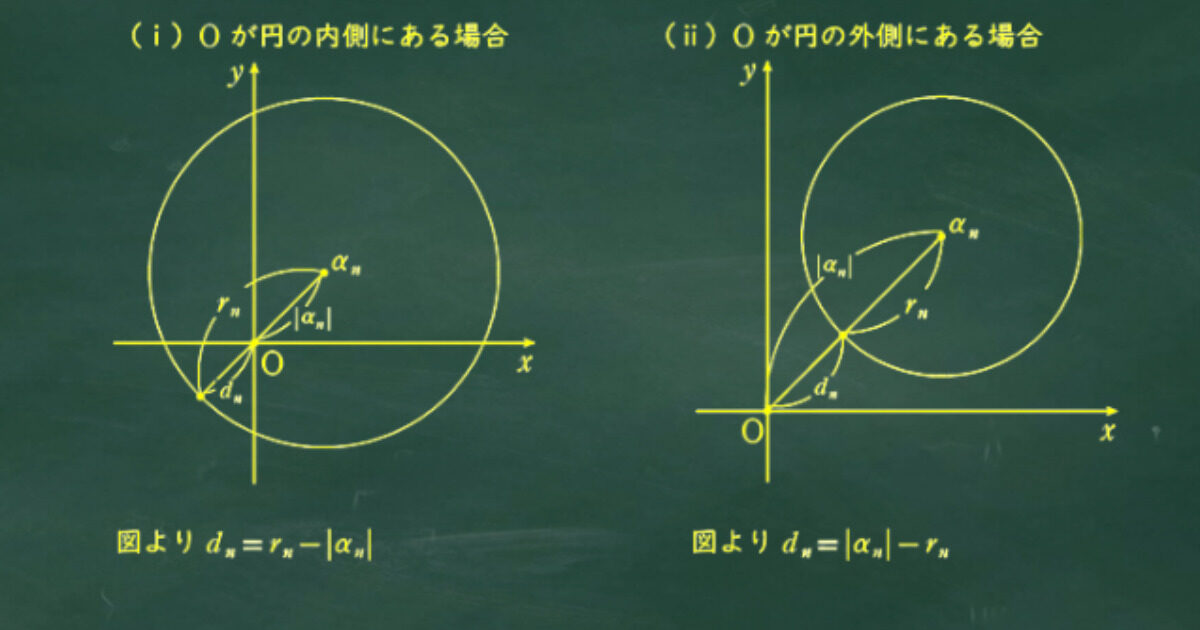
O が円の内部にあるときと外部にあるときで場合分けが必要。

ここで、図を用いてd_nを考えよう。

次の２通りで場合分けを行う。

ｎ の値によって以下のような答えとなる。

最後の極限値の問題はそんなに難易度が高くないので、式をしっかり求めておけば完答できる。

終わりに

複素数平面の問題だが、数列の漸化式や極限などの他分野との融合も入っている。

このような融合問題は入試の過去問を利用しながら経験していくことが大切なのでしっかりと練習しておこう。