参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2024東北大大問4(理)
問題

数学C(旧課程では数学B)の空間ベクトルの問題。
球と球の交線を通る平面の問題から始まり、平面間の距離まで求めるかなり難易度が高い問題。
(1)、(2)くらいまでは何とかなるが、(3)、(4)は空間図形の問題に慣れている必要がある。
この解説をしっかり読んで空間図形に強くなれるよう対策を立てよう。
解説
(1) の解説
これはしっかりと解きたい問題。
2点間の距離の空間バージョンだ。
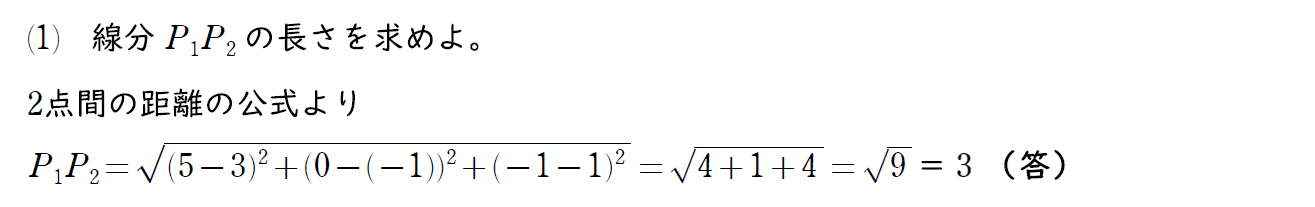
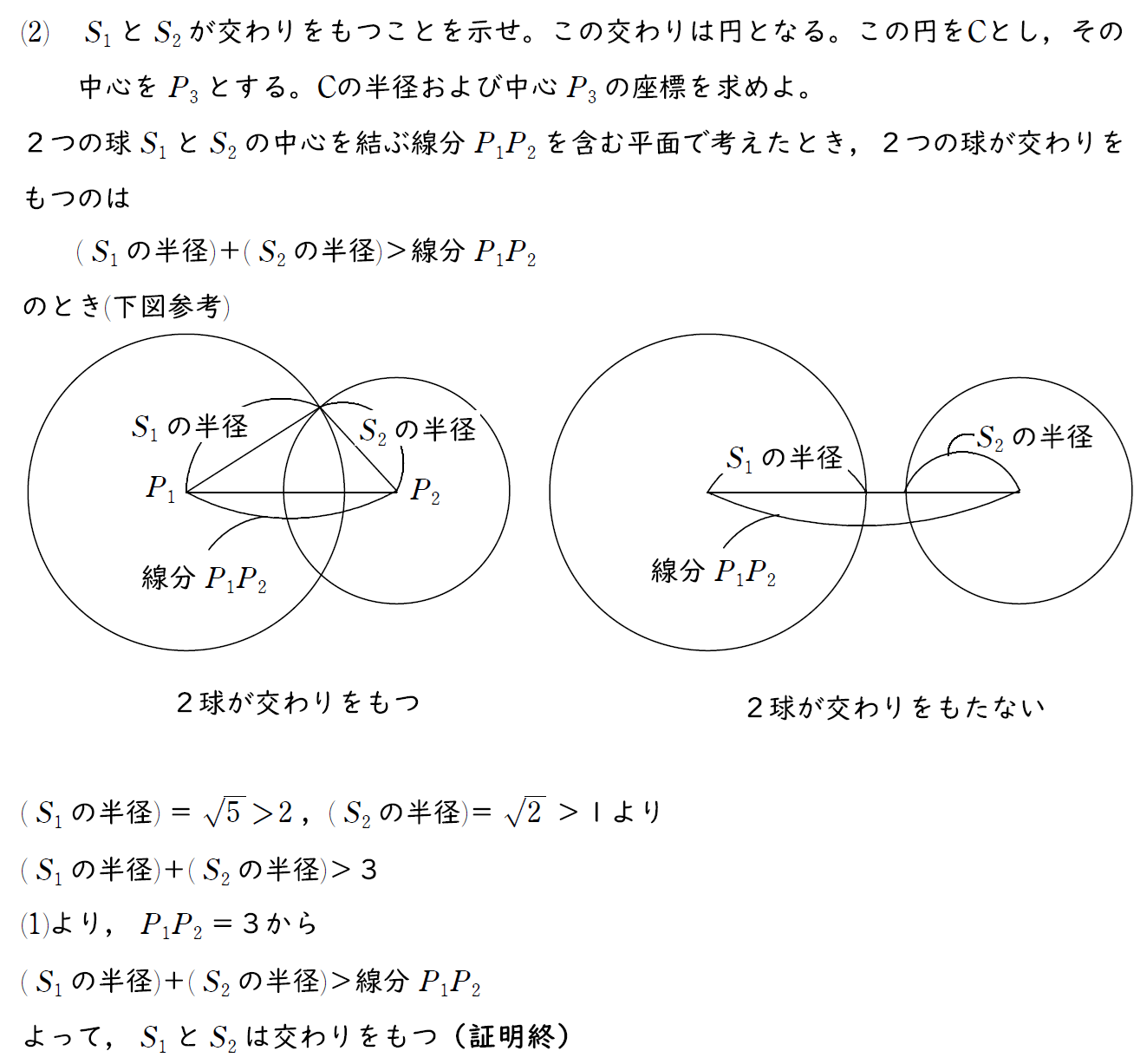
(2) の解説
2つの球の交わりを示すのは数学Aや数学Ⅱの「2円の位置関係」を使って説明する必要がある。
空間図形は平面に落とし込むのが解答の筋道だ。
円の中心と半径を求めるのに、引き続き平面に落とし込んで考える。
ここでは初等幾何の考え方で説明したが、点と平面の距離や法線ベクトルの考え方も使える。

(3) の解説
平行でない2つの平面と平行なベクトルは、2つの平面が交わってできる直線と平行であることを意味する。
ここでは平面の方程式や法線ベクトルの考え方を使おう。

(4) の解説
これは問題を理解しイメージするところから難しい。
以下の解答のようにざっと図を書いて問題を把握していこう。
その後、やはり平面に落とし込んで初等幾何で考えてみよう。
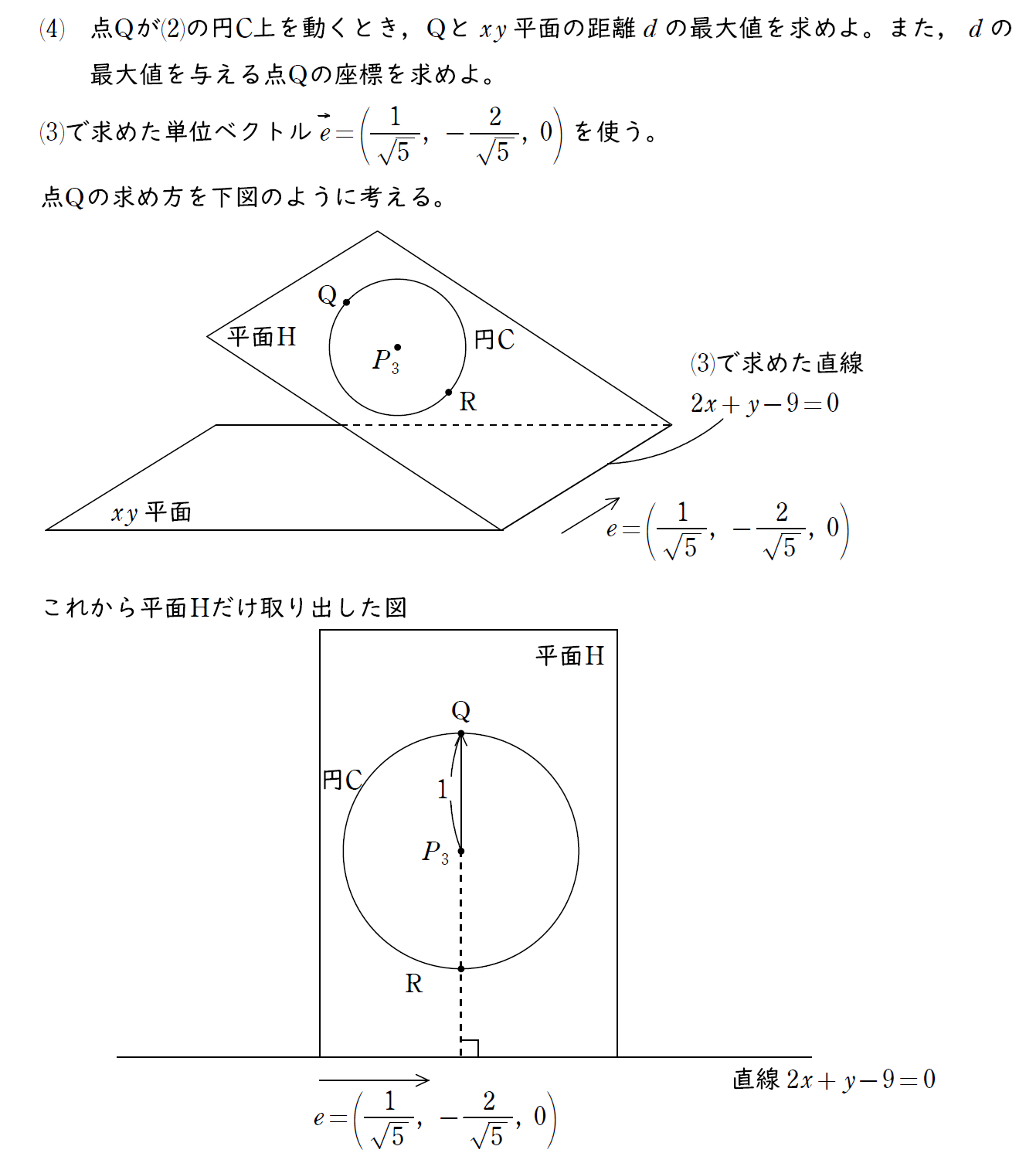
円周上の直線から最も近い点、最も遠い点はベクトルではよく見かける問題。
円の中心を通り、直線に垂直な線を引いて考えよう。

上のように答えが2つ出てくるのだが、これは最も近い点と最も遠い点の2つが考えられるからだ。
そのどちらかを決定するのは実際に距離を求めてみるとよい。
その距離はxy平面までなのでz座標だけで求めることができる。ただし、絶対値を忘れないように。

終わりに
この大問4のベクトルの問題は、近年の東北大の中でも難易度が高い方といえる。
特に空間図形が苦手な受験生も多いので、しっかり解説を読んでマスターしてほしい。
空間図形は他にも数学Ⅲの積分分野における「立体の体積」でも頻出だ。









コメント