参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022千葉大大問3
問題


これは絶対値の問題ね

絶対値は場合分けが必要だよ。頑張って場合分けしてグラフを書いてみよう
この問題で大事なことは次の3つ
- 絶対値の入った関数はしっかり場合分けを行いグラフを書く
- 交点の数はグラフを見ながら判断する
- 積分計算は文字が入ると煩雑になりミスしやすいので見直しをしっかり行おう
この問題では「放物線と直線の間の面積を求める」いわゆる 1 / 6 公式を使うよ。
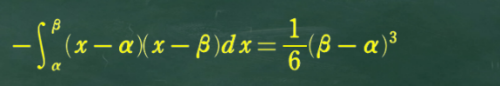
解説
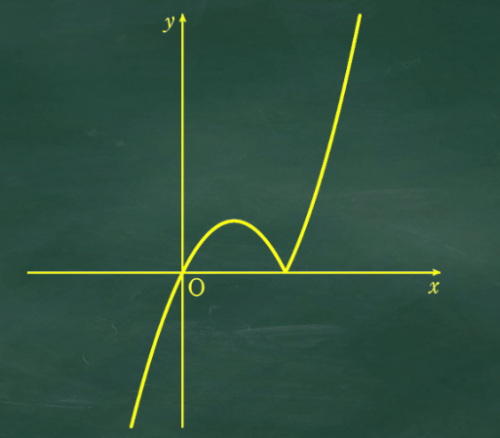
(1) の解説
まずはしっかりグラフを書こう
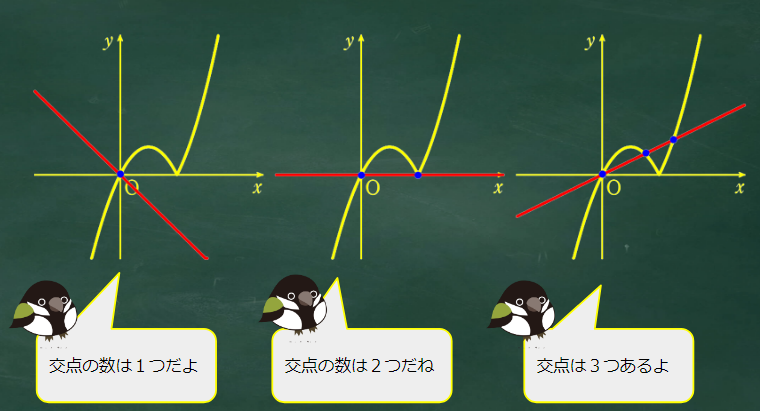
直線の交わり方は次の3つ

放物線のグラフを書くときは平方完成して頂点を求める場合が多いけど、この問題は x 切片を求める形のほうがグラフが書きやすいよ。
①のグラフを書くと
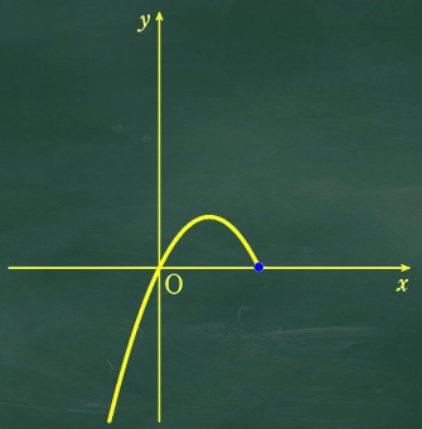

②のグラフを書くと
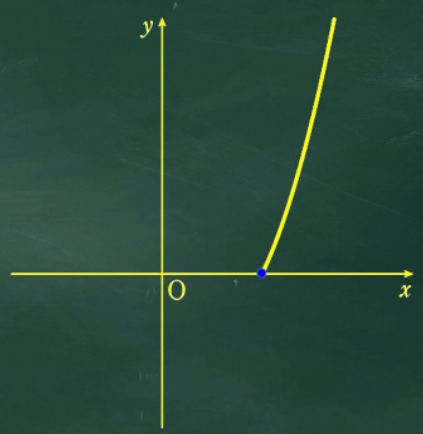
①と②のグラフを合わせるとグラフはこんな感じ
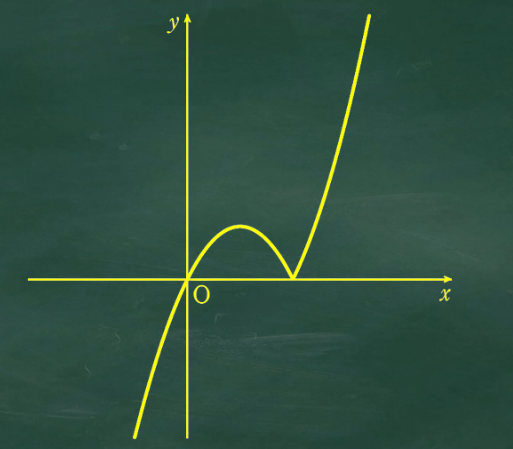


まずは a の値を正と負で分けてみない?

いいね。a が負だと1点でしか交わらなさそうだね。グラフで確認しよう!
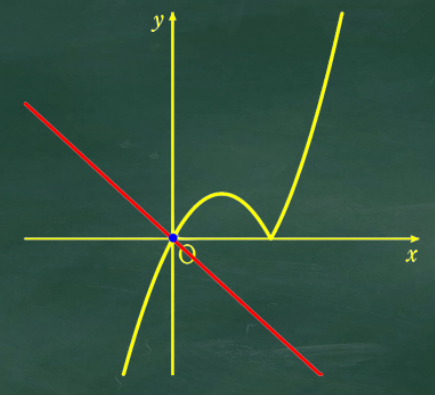


a =0のときはどうかしら?
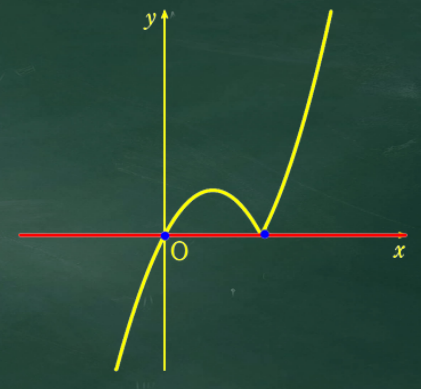

図をみると交点の数は2個だね

他にも交点の数が2個の場所がありそう?

原点で放物線と接するときが怪しいね
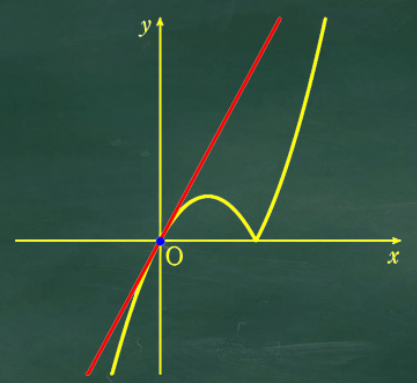


a の値が0と2の間のときの交点の数は3個ね

正解!あとは a が2より大きいときだね
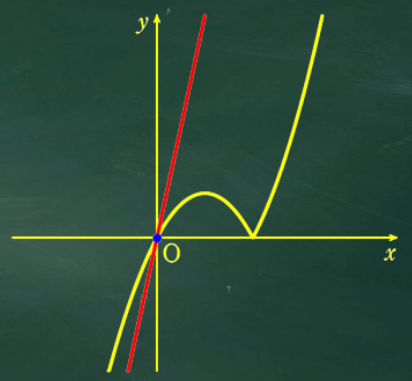

図を見ただけではちょっとわからないね

交点の数がわからないときは式を連立して交点があるかないかを調べてみよう。
(2) の解説1

(2) の問題の a の範囲は (1) の2点か3点で交わるときの範囲ね

とりあえずこの範囲のときのグラフを書いてみよう
(1) で求めた交点も使ってグラフを書くと次のようになるよ。
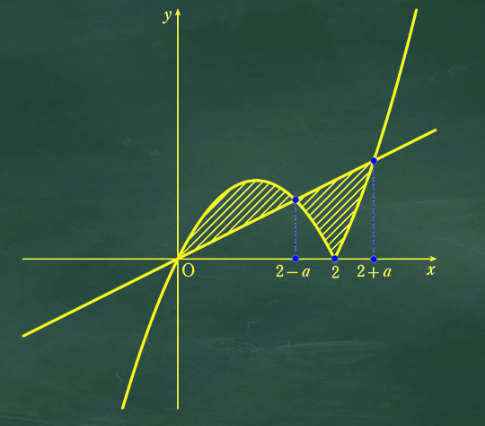
図の斜線部分が求める面積だね。
あとは積分を使って面積の値を求めればいいね


結構計算が大変だったけどとりあえず答えが出たね。
(2) の解説2
解説1では積分の計算がとても大変だったね。

1 / 6 公式が使えるともっと楽に計算ができるのにな
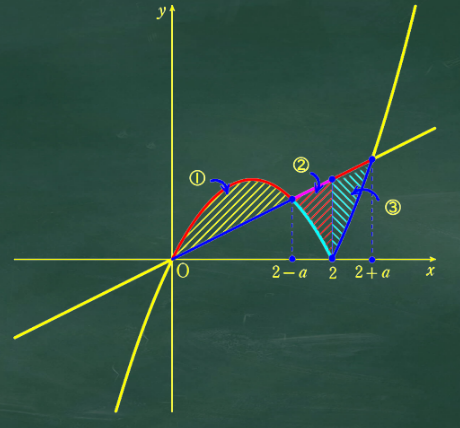
次の図の考え方が理解できたらすごく楽に解けるけど考え方が難しいよね。
興味があったらチャレンジしてみてね。
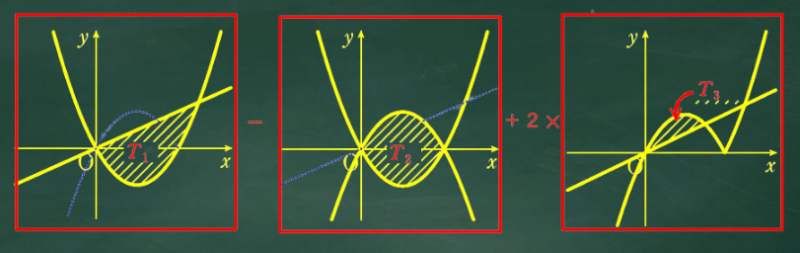

絶対値のグラフはx軸で折り返すものが多いけど、折り返す前のグラフを利用すると面積は求めやすい。
(3) の解説
(2) まで解けてると(3) はすぐにできそうだね。やっぱりこの問題も (2) で計算ミスをしないことが大事だね。

終わりに
数学Ⅱの微分積分の範囲では文字の入った2次関数や3次関数の問題が多いよ。
中でも絶対値の問題は場合分けをうまく行ってグラフで考える必要があるのでしっかり演習をして対策を立てよう。
あとは定番の「接線」「増減表」「面積」の問題を押さえておけばいいと思うよ。









コメント