参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022大阪公立大大問1(理系)
問題


数学Ⅲの問題ね。少し難しそう。

数列の極限や微分、積分のいろいろな知識が必要そうだね
この問題で大事なことは次の3つ
- グラフを利用した不等式の証明ができるか。
- はさみうちの原理を使って数列の極限が求められるか。
- 定積分を利用した不等式の証明ができるか。
解説
(1) と (3) は「不等式の証明問題」で、これは教科書で扱う例題の中にあるよ。
この後、丁寧に解説するのでしっかりマスターしてね。
(1) の解説

「グラフを利用した不等式」の問題ね。

よく気付いたね。数学Ⅱでも使う証明法だから数学Ⅱの教科書の例で復習しよう。
↓ グラフを利用した不等式の解説だよ。

ここから (1) の解説だよ。

(2) の解説

この極限はどうやって求めるのか解き方が全く思いつかないわ。

かなり難しい問題だよね。この手の問題は入試問題にありがちなんだけど (1) が誘導になっているんだね。
(1) をうまく使って「はさみうちの原理」で極限を求める問題だよ。
まずは「はさみうちの原理」から説明するね。

ここから (2) の解説だよ。

(3) の解説

これは「定積分を利用した不等式」の証明ね。

その通り。まずは考え方を復習しておこう
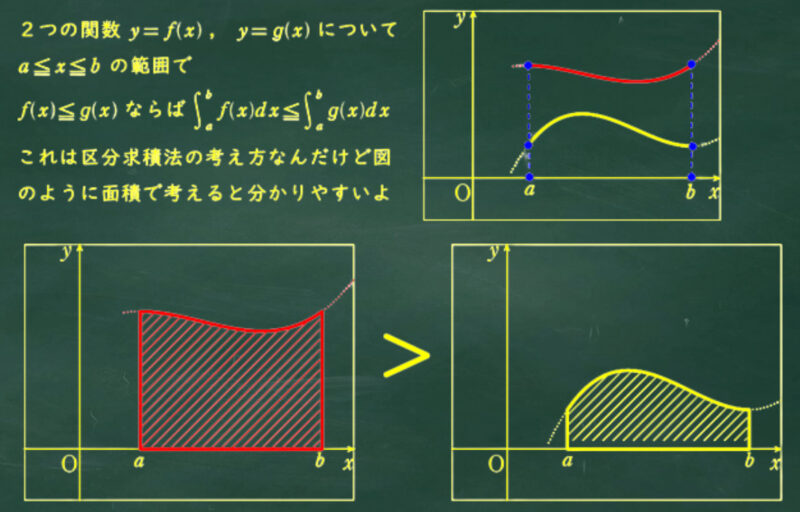
この問題の難しいところは積分するもとの不等式を問題を見て自分で考えることだね。
まずは方針を立てるところを説明するよ。

ここから (3) の解説だよ

終わりに
今回の問題のように (1) から (3) までが全て関連しているときは次のことの注意しよう。
- 前にある小問が誘導になっていないかを見極める。
- 前にある小問の答えが間違ってると次の問題に大きく影響するので注意。
この問題では (1) を使って (2) を解くんだけど (1) ができていなくても (2) には進んでいいよ。
(3) は (2) の答えを使うので (2) の時点で答えがあっていないと (3) を解くことはできないよね。
とにかく解説の中にも書いてあるけどこの問題みたいな証明問題が解けるようになるには「教科書」の例題をしっかりよけるようになることが最も大事だよ。
過去問に取り組む前にしっかり教科書をマスターしよう。









コメント