【2022】神戸大学入試問題数学大問１(理系）をとことんわかりやすく動画を使わずに解説します

参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか？

YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。

この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。

2022神戸大大問１（理系）

問題

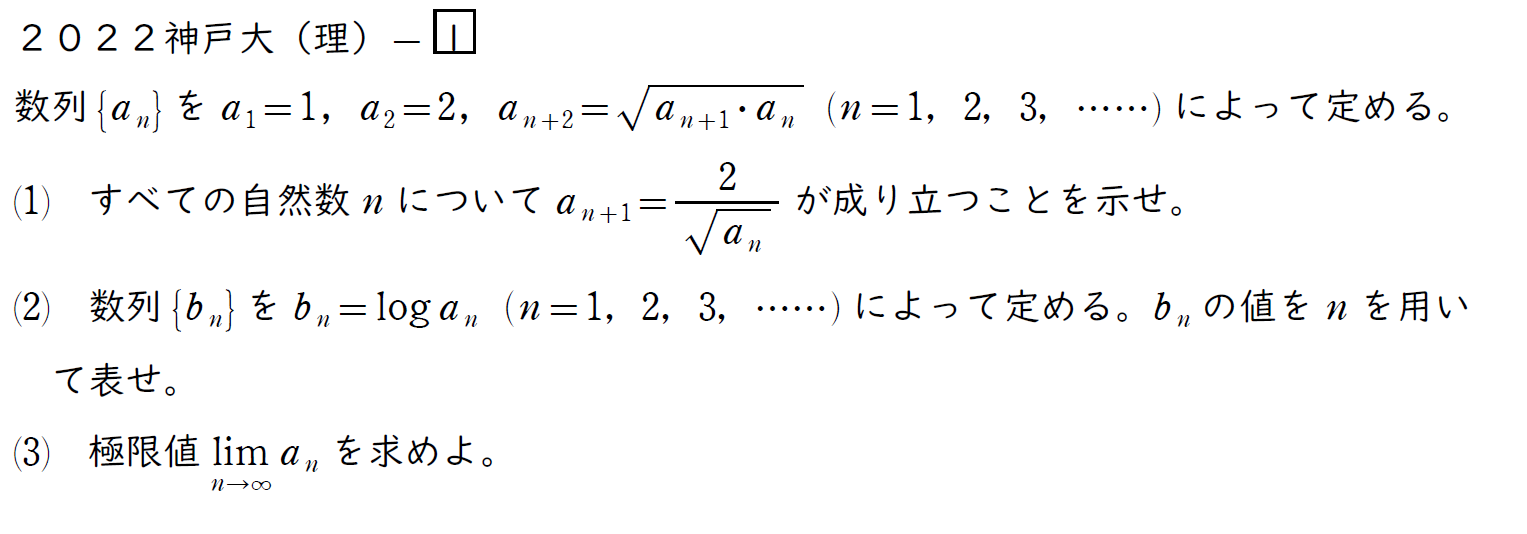
次の３つのことを意識しよう。

解説

数学 B の数列の問題だが (2) では数学Ⅱの対数、(3) では数学Ⅲの極限と複数の分野にまたがった問題。

(1) の解説

ここでは２つの解法を紹介します。

解答１

漸化式にはいろいろな変形方法があってその解法を覚えることが多いが、この問題のように見慣れない漸化式の場合は変形に工夫が必要。

したがって問題文ある漸化式に何らかの変形を加えて (1) の形にすることが必要となる。

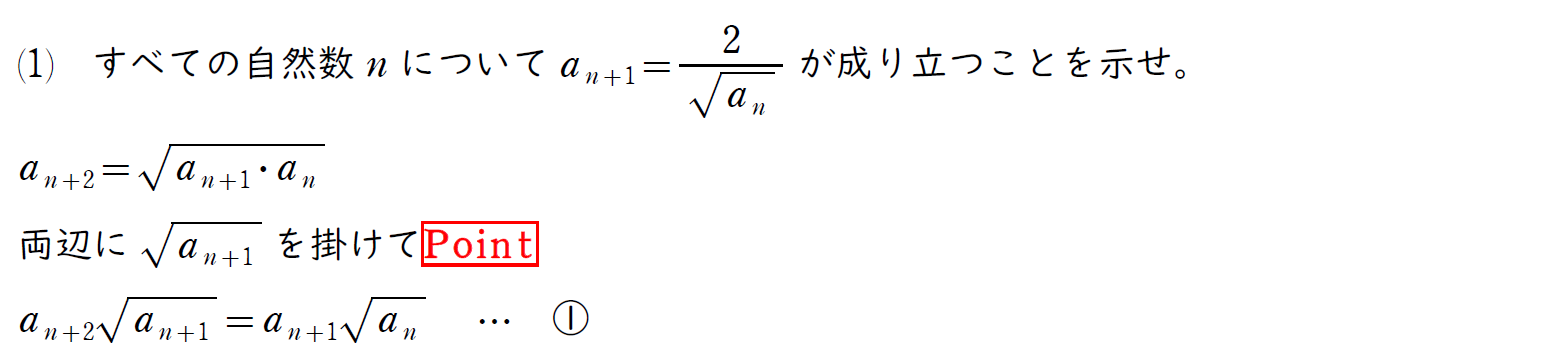
この Point の部分で両辺に何を掛ければいいのかが難しい。この場合 ① の式が

と形が整うことを目標に変形して考えるのだが…，難しいね。

これに気づけば後は番号を下げていく（これは漸化式を解くときによく用いる方法）。

解答２

漸化式の証明では数学的帰納法を用いることが多い。

漸化式に限らず数列の分野ではこの帰納法が重宝されるので困ったときには帰納法を用いることを考えてみよう。

(2) の解説

この問題は無理数の入った漸化式でよく見かける「対数をとる」の誘導問題となっている。対数をとるときは真数条件に気を付けよう。

この漸化式は教科書でも一番使う形。

ここで変形方法を確認しておこう。

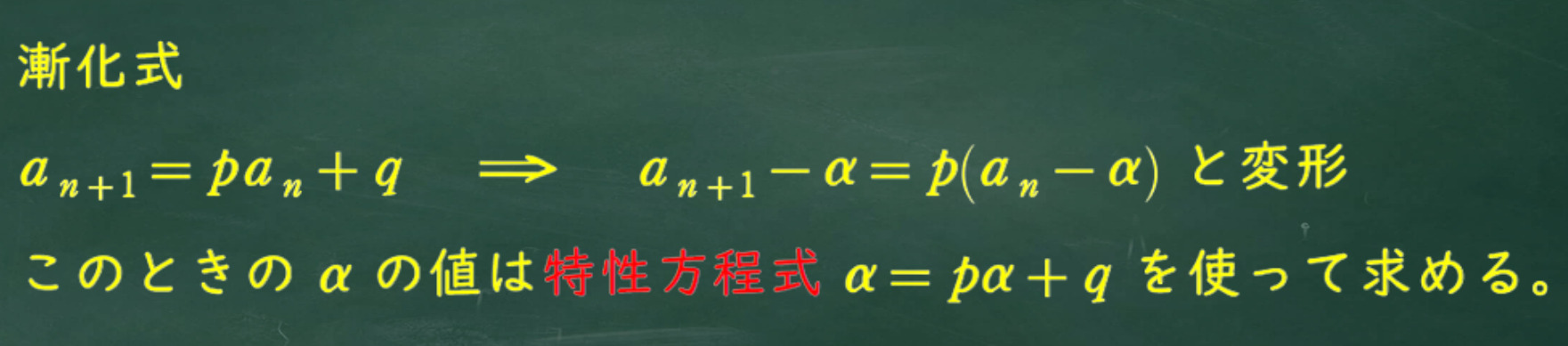
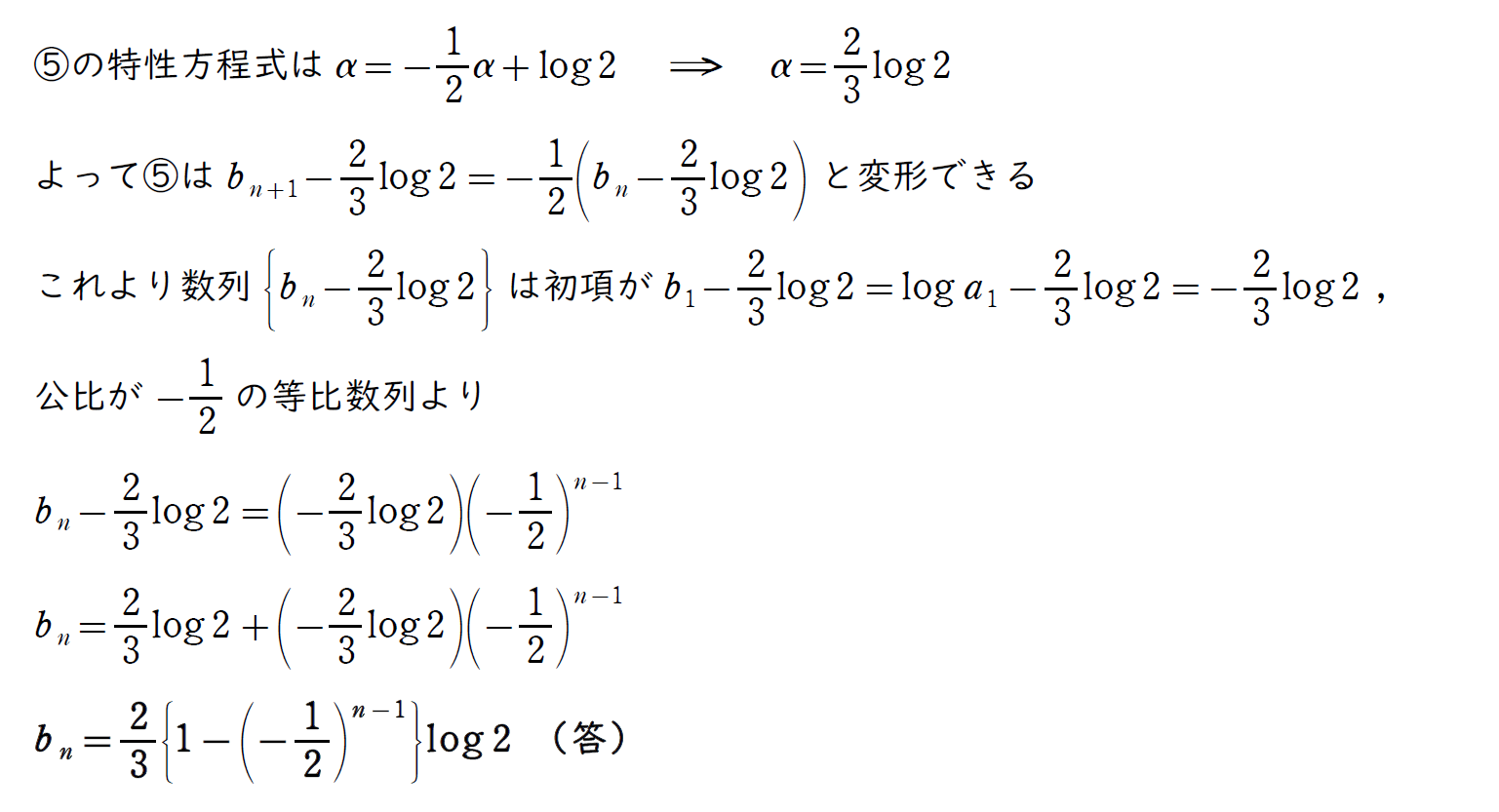
(3) の解説

(2) が求まれば (3) はそんなに難しくない。

数列の一般項に対する極限の問題ではよくあるパターンだが、完答するためには (2) でミスしないことが大切。

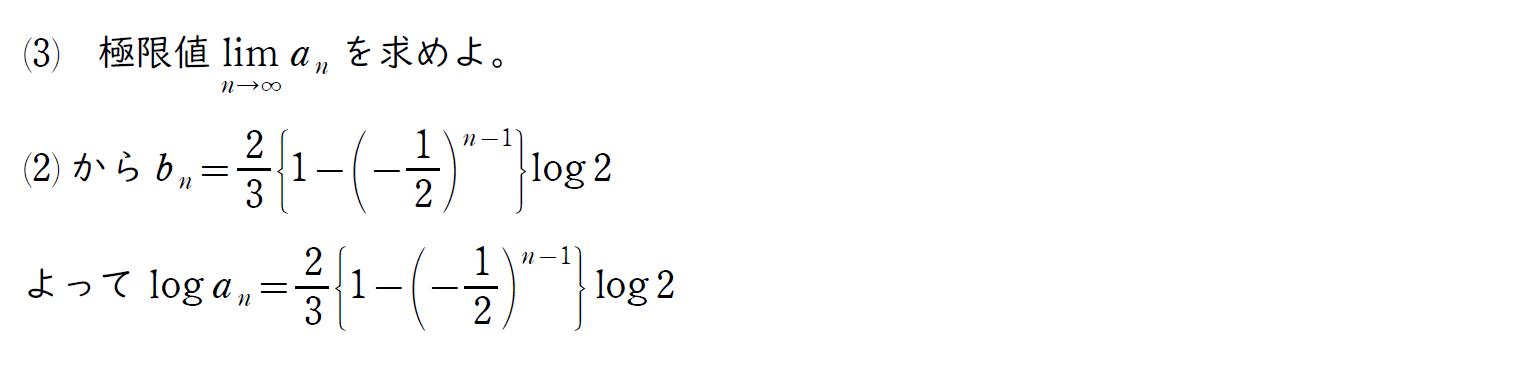
対数の性質を使って変形。

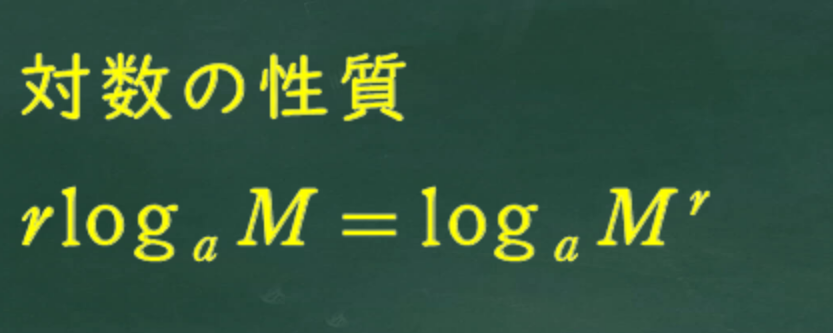
終わりに

漸化式の問題は問題集にあるよな定番の問題からこの問題のように変形に工夫が必要な問題まで様々ある。

(1) の証明がうまくできなくても (2) では漸化式の定番の形への変形を誘導してくれているのでしっかりと完答したいところ。

数学的帰納法は数列の証明問題によく使われるのでしっかりマスターしてほしい。