【2022】神戸大学入試問題数学大問３(理系）をとことんわかりやすく動画を使わずに解説します

参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか？

YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。

この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。

2022神戸大大問３（理系）

問題

(1) は極値を求める問題なので微分をし、増減表を作って求める。

(2) はすぐに a の値が定まるのでグラフを書いて、求める面積部分を確認し積分を使って求める問題。

この関数が「偶関数」であることに気づけば (1) (2) とも少し計算が楽になる。

解説

(1) の解説

式に文字が入っているが、場合分けを行う必要はない。

a の値の範囲に気をつけながら増減表を作ってしっかり考えよう。

偶関数であることに気づけば増減表は半分ですむが、気づかなくても問題はない。

ここでは偶関数であることを用いず解説をする。

(2) の解説

条件から最初に a の値が定まる。グラフは (1) で調べた増減表を使うと考えやすい。

問題文の条件からx 切片もわかることに気づきたい。

ここでは計算が大変なので偶関数を用いて計算する。

y=f(x)が偶関数であることを確認し、式を半分にする。

この定積分は「部分積分法」を用いるのでまずはその確認から。

偶関数・奇関数の定積分

部分積分法の確認

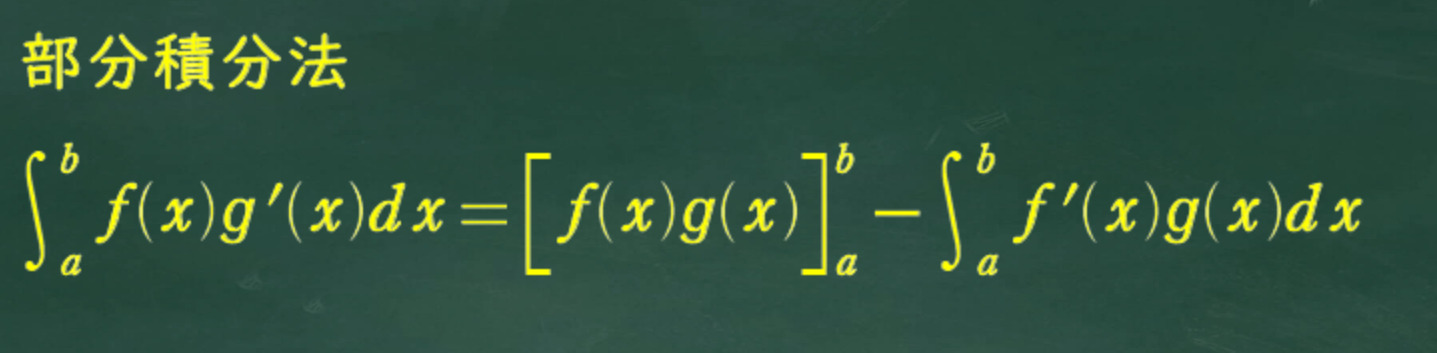
式の中に厄介な置換積分が含まれている。

教科書や問題集では鉄板のtanθを利用した置換積分。

本番の解答でもここで示した方法の煩雑になる計算部分から部分的に取り出して取りだして解答を作るとよい。

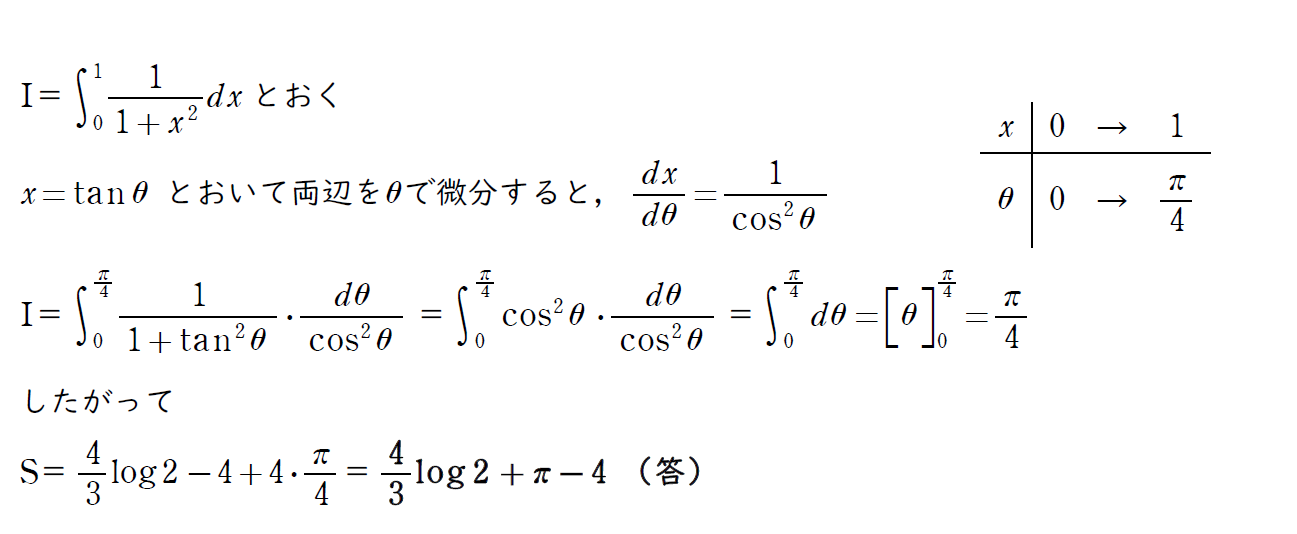
終わりに

積分を使った面積の問題はグラフをしっかり書くことが重要。

ここでは (1) で増減表を作らせる誘導があったが、誘導がない場合は、増減表にこだわらずグラフの大まかな位置（ｘ軸や他の曲線との上下関係）だけでもしっかり押さえておけば時間短縮ができる。