参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2023京都大大問5(理系)
問題

数学Ⅲの微分積分の問題。
いわゆる通過領域の問題だが、それを回転体の体積と組み合わせて出題されているため、慣れていない受験生にとっては厄介に感じるかもしれない。
まずは通過領域の問題として取り組むところから始めよう。
解説
点Pはx軸上を動くので考えやすいが、点Qがyz平面上をくまなく動くので考えにくい。
そこで以下の解法にある通り点Qがy軸上にあるときで通過領域部分を考える方針が必要だ。
さらに計算を簡略化するために、2点P,Qの存在範囲をx、y軸の正の部分に断定して考えるとよい。

通過領域の問題でよく使われる「パラメータ変換」を考える。
回転体の体積にはx=t平面における断面積を求め、そのtを動かすことに求めるのだが、いったん通過領域の問題として考えるため、tを定数として固定する。
あとは立体の一番外側を作る部分を考えるため、軸から一番遠い部分、つまりy座標の最大値を考えればよい。

終わりに
一時期いろいろな大学で出題された通過領域の問題と今も理系の問題として頻出である立体の体積問題の融合であるこの問題は受験勉強の演習としてうってつけだ。
このような良問を解きこんで、受験に必要となる頻出分野の解法の知識を手に入れてほしい。
難易度はやや高いが解説をしっかり読んでマスターしよう。







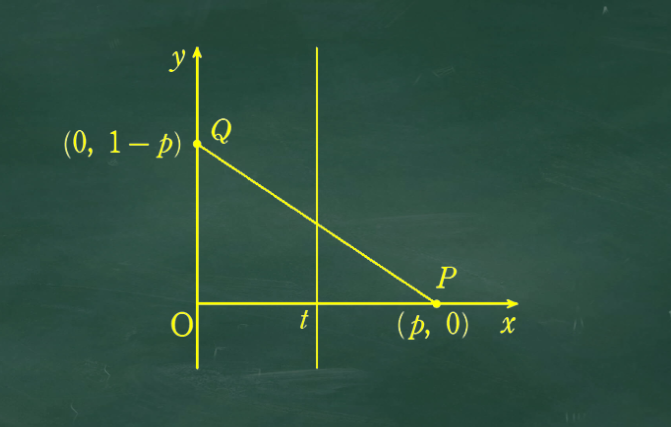


コメント