参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022九州大大問5(理系)
問題

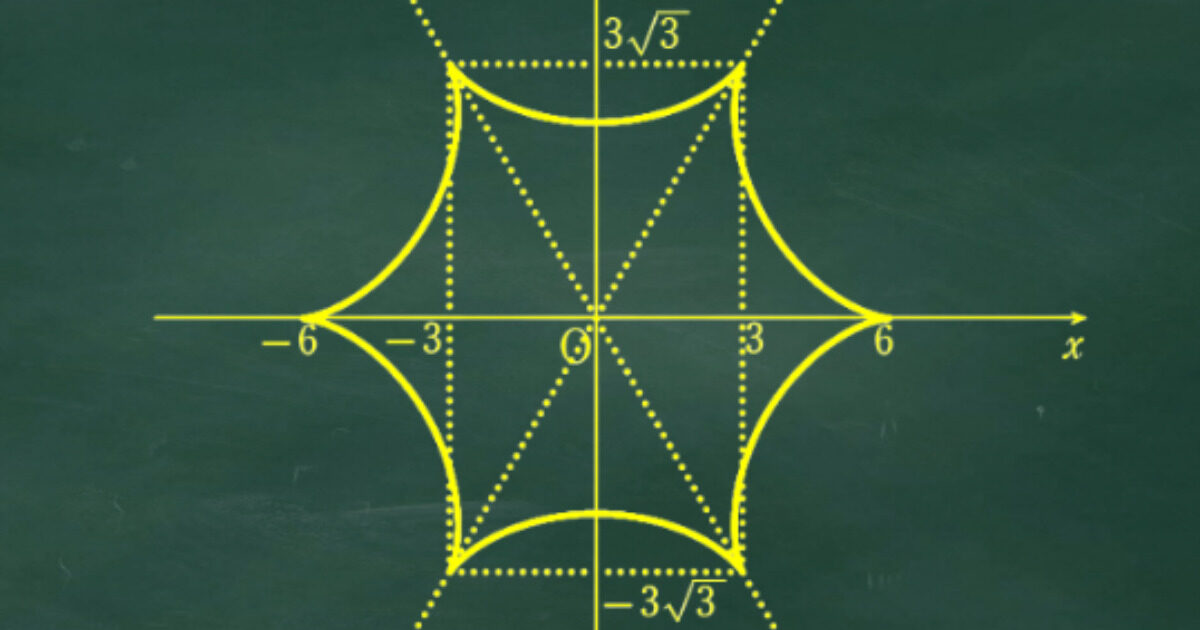
媒介変数で表された曲線の問題。
あまり見かけない曲線なので概形のイメージがわかないが、誘導に従ってしっかり考えていけば最後までたどり着くようになっている。
ただし、計算部分も含めてかなり難易度が高いので、以下の解説をしっかり読み、まずは解き方を理解するところから始めてほしい。
解説
(1) の解説
まずはx、yをそれぞれ微分してその符号を調べるもの。
この解答の中では三角関数の和積の公式を使用する。
まずは三角関数の和積の公式の確認から


媒介変数表示された関数の微分法を用いる。
まずは公式の確認から。


(2) の解説
(1) の誘導を用いて媒介変数表示された曲線のグラフを書くために増減表を作る。
その後、グラフを書いて求める面積部分を確認する。
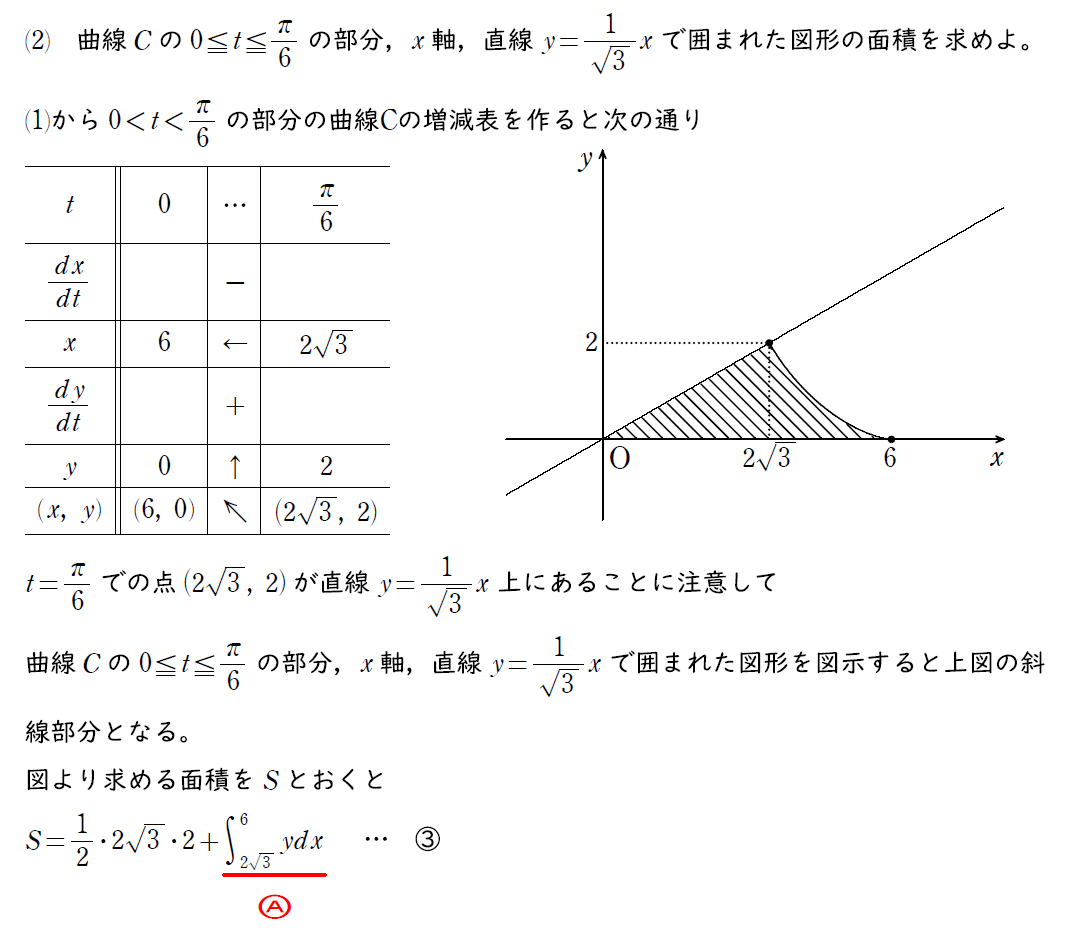
面積を求める式を立てることが出来たら、次は媒介変数の積分式を計算する。
解説のように積分する部分だけを取り出して計算しよう。
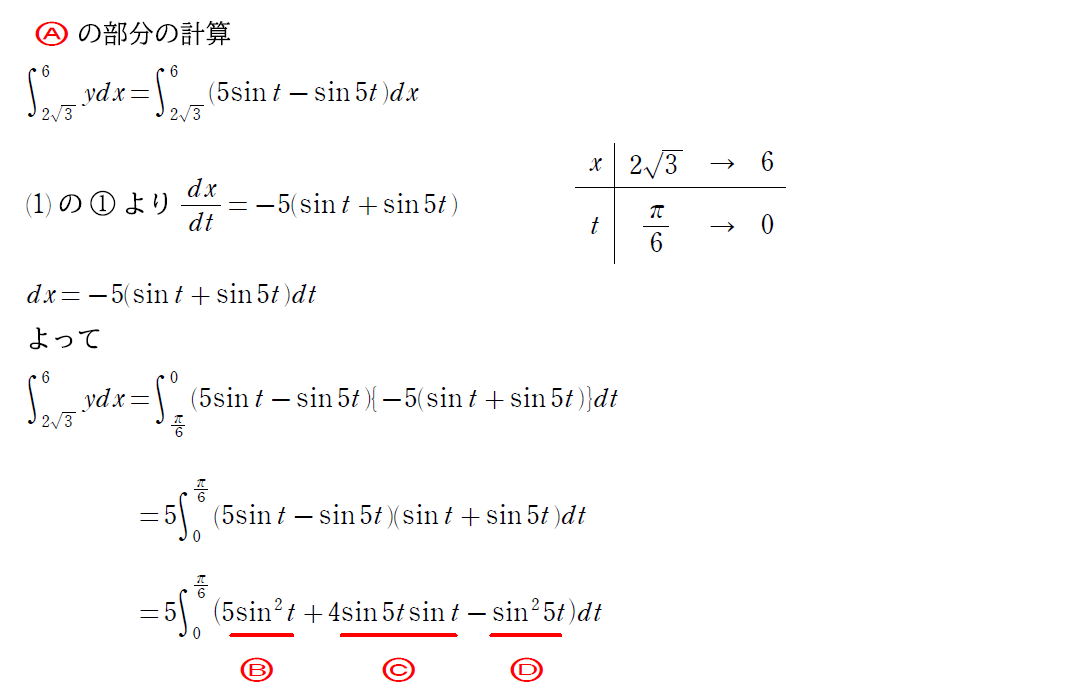
この先の計算を進める上で、三角関数の半角の公式と積和の公式を用いる。
それぞれの公式を確認しておこう。
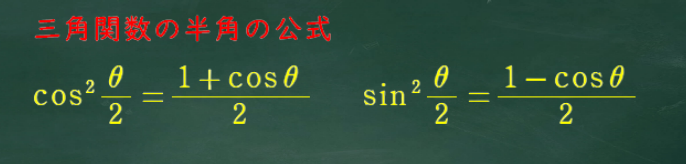


(3) の解説
x軸対称、y軸対称、原点対称はよく出てくる内容だが、三角関数の媒介変数表示でこの対称性を考えるには少しコツが必要だ。
三角関数の媒介変数表示における対称性を証明するのに必要なものをここでまとめておこう。


~を回転させてという部分には複素数平面を利用する。
他にも行列計算を用いる方法もあるが、現行の高校教科書には出てこない。
回転を表す複素数の公式を確認しよう。


途中でコメントが入っている角度をそろえる部分は少し気づきにくいかもしれない。
X 座標と同様に Y 座標も変形していく。

(4) の解説
(3) でx軸対称は説明しているので、最初にy軸に関して対称かどうかを確認しておく。
対称性の確認方法は↑を参考に。

(2) で0≦t≦π/6 部分の増減表を作りグラフを書いたが、これでは不十分。
グラフの概形をしっかり書くためには凹凸を調べる必要があるからだ。

(3) で60°回転すると重なることが分かっているので、x軸対称、y軸対称であることも考慮してグラフを書く。
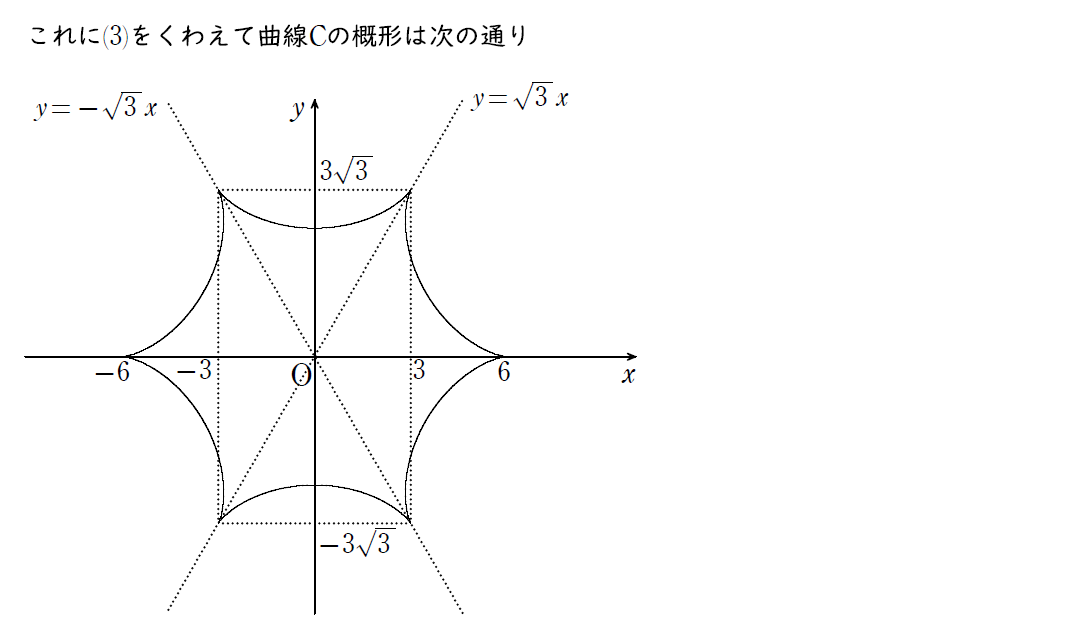
終わりに
媒介変数表示された曲線の問題は大学入試問題によく取り上げられる。
問題集や参考書でもよく見かけるが、この問題のように難易度の高いものはあまり見かけない。
特に複素数平面を絡めた部分は今後も他の大学でも出題される可能性もあるので練習しておきたいところだ。








コメント