参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022大阪公立大大問4(理系)
問題


媒介変数tを使って表される曲線の問題ね。

難しそうだけどグラフを与えてくれているから問題は理解しやすいね。
この問題で大事なことは次の2つ
- 三角関数の様々な公式を使う問題なので教科書に載っている公式をしっかり覚えておく必要がある。
- 媒介変数表示された曲線の接線の傾きを求めるためにその導関数が必要になる。
解説

この問題の前半は等式の証明の問題ね

まずは等式の証明方法を復習しておこう。
等式の証明には次の3つの方法があるよ。

(1) の解説
ここで使う三角関数の公式は加法定理だよ。

(2) の解説

この問題も(1)と同じ方法で証明すればいいね。

そうだね。でもこの証明は途中の変形が難しいので (ⅱ) の証明方法を使って説明するよ。

このまま左辺の変形を続けてもいいけど、少し複雑なのでここでいったん止めておいて右辺の変形をするよ。
入試本番でもこのように臨機応変に対応する練習をしておくと、行き詰った後も解答を続けることができるようになるよ。
ここで使う三角関数の公式は半角の公式と積を和の形に直す公式だよ。

(3) の解説

ここからは曲線の接線の問題だから微分を使うのね。

そうだね。接線の公式と媒介変数で表された曲線の導関数を求める公式をチェックしておこう。
微分を利用した接線の方程式は次の通り

媒介変数表示の導関数は次の通り
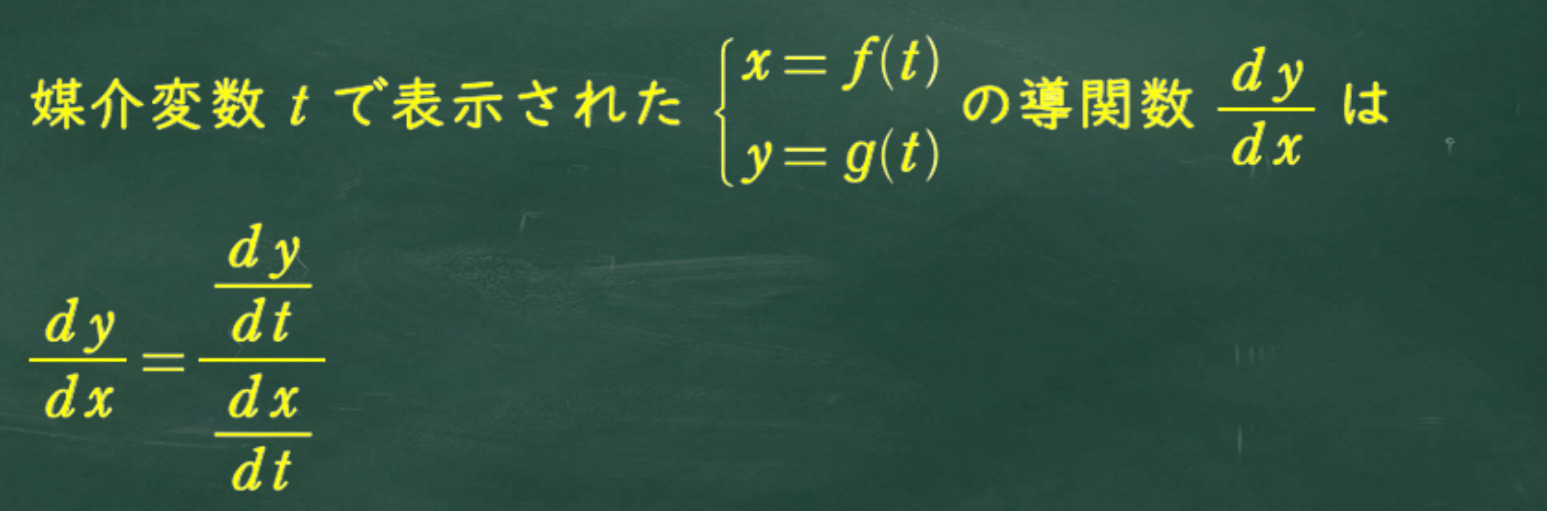
ここから(3) の解説だよ。

ここから先の変形が難しいよね。tanθと形を合わせるには半角の公式と2倍角の公式をそれぞれ次のように分母、分子に使おう。
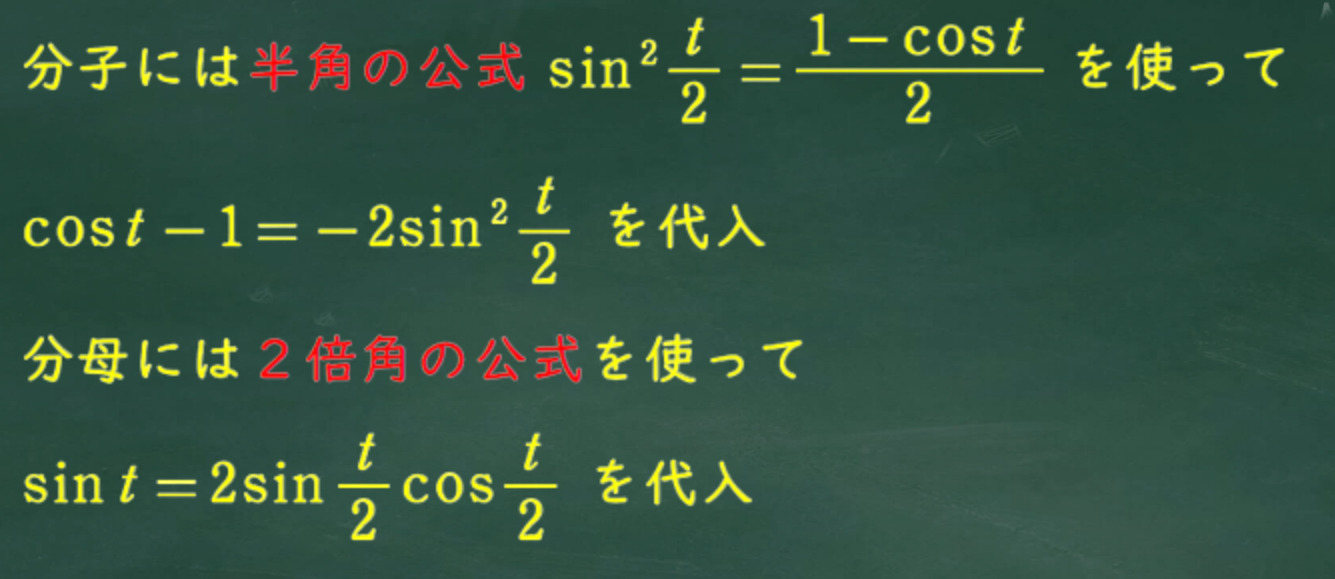
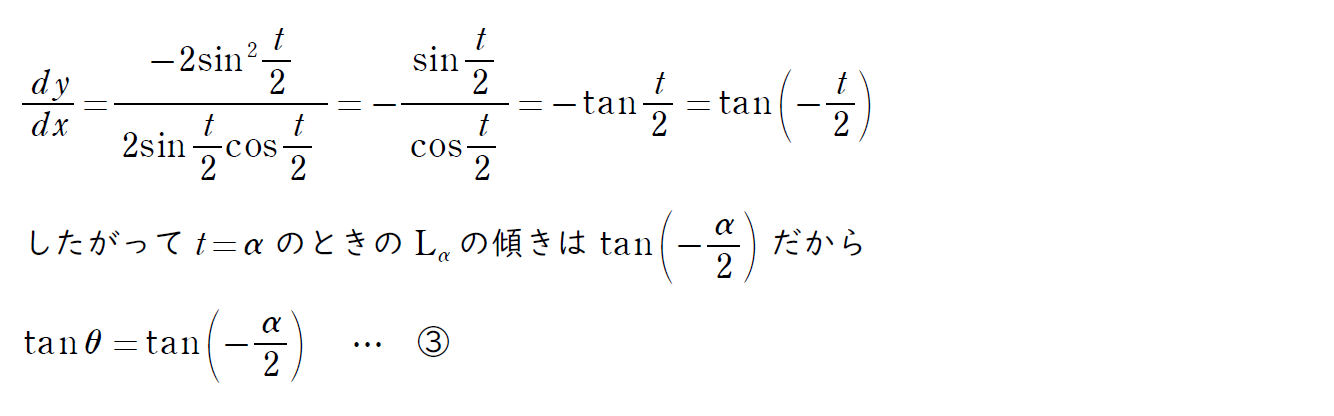
ここで θ の範囲と α のの範囲をそれぞれ考えるよ。

(4) の解説

「α によらず一定」は α が入っていない式にできれば完成ね

P1P2 の長さを求めてその中にαが含まれていなければ証明は終わりだね
まずは接線の方程式を求めて少しだけ変形しておこう

次に2点 P1,P2 の座標が必要なのでそれぞれ求めるよ。
まずは P1 の座標から

結構大変だよね。次は同じようにして P2 の座標を求めるよ。

最後に2点間の距離を使って P1P2 の長さを求めるよ。

終わりに
この問題も前半部分が誘導になっていて後半の問題にそれを使うという形だね。
式を変形するときに三角関数の公式を多数使うのですべての公式が頭に入っているようにしたいね。
特に積を和の形にする公式や π-θ の関係式などを覚えていない人が多いのでよく復習して使えるようにしておこう。










コメント