【2024】横浜国立大学入試問題数学理系大問５をとことんわかりやすく動画を使わずに解説します

参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか？

YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。

この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。

2024横浜国立大大問５（理）

問題

この問題は様々な分野の融合問題。主に数学Ⅲの極限と微分を使う。

問題に図が入っているので、把握はしやすい。

(3)の証明あたりから難易度が上がるので、まずは(1)、(2)の完答を目指そう。

解説

(1) の解説

まずは三角比の余弦定理を使って求めていく。

式の変形には２倍角の公式も用いる。

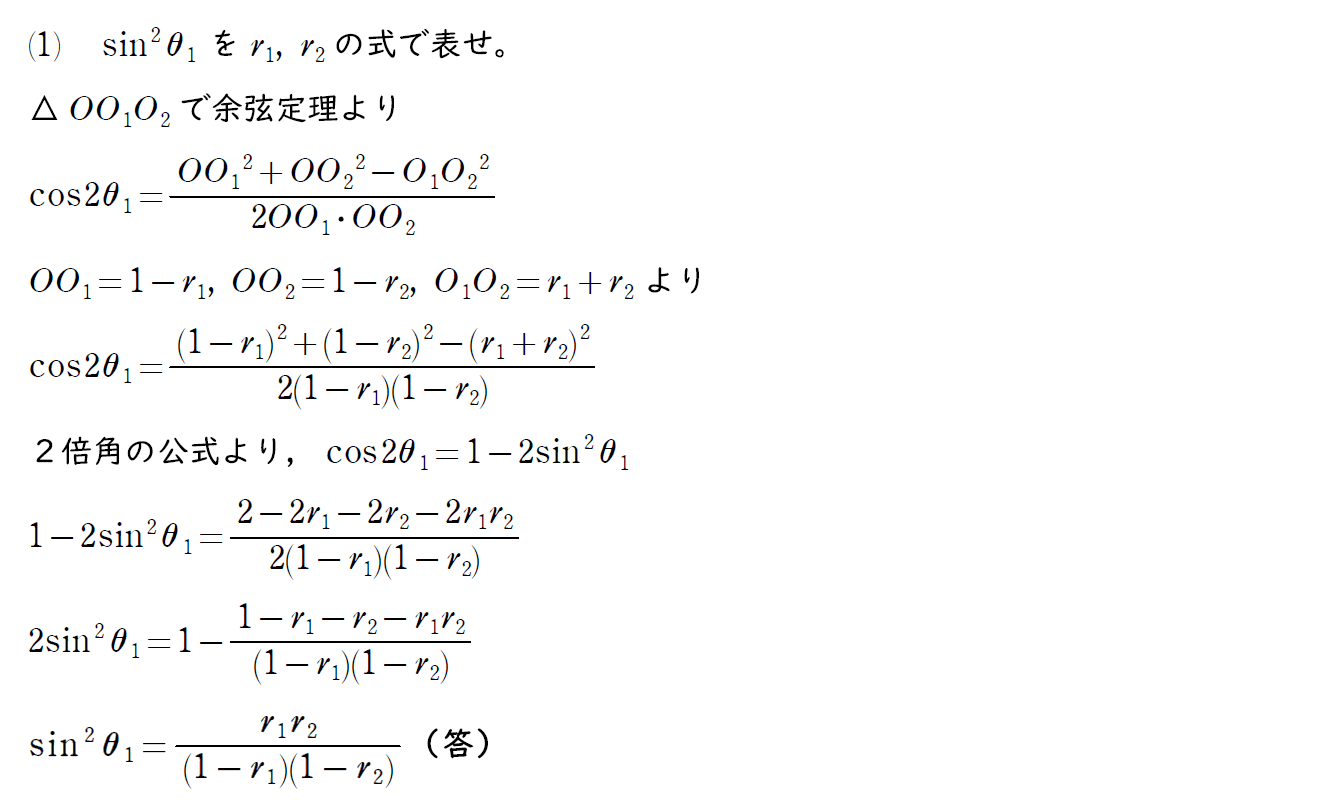
(2) の解説

ｎ番目の図形も１番目と同じなので(1)が誘導として使える。

あとは条件を代入して指数計算を行う。

(3) の解説

ここからは大幅に難易度が上がる。

不等式の証明のセオリーとして（右辺）ー（左辺）を計算して示していくのだが、ここでは微分を用いて増減表を作りグラフで考える必要がある。

計算がとても複雑になるので、平均値の定理を用いて極値を調べることにした。

多少、解説が分かりにくいところもあるかもしれない。

ここからは直接ｙ＝０の解を求めてもいいかもしれない。

解説では解を求めず、平均値の定理を用いて０＜ｘ＜π/６に解が存在するかを調べた。

増減表から範囲の両端の符号を調べる。

ｘ＝π/６のときの値の符号が求めにくいのでしっかり計算を進めよう。

(4) の解説

極限の問題ではさみうちの形を計算する。

内容は無限等比級数の問題なのでそれほど難しくはないが、(3)同様計算が複雑なので最後までたどり着くのが大変かもしれない。

終わりに

この問題は難易度が高く、計算量も多い。

完答を目指すよりも取れる部分に集中し、部分点狙いで十分だろう。

むきになって解いていると時間的にも不足しそうだ。