参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022横浜国立大大問2(文系)
問題

文字の入った3次関数だが、f(x) と g(x) を連立したグラフを書くことが攻略の糸口だ。
慣れていないと難しく感じてしまうが、国立の入試問題で3次関数が出題されるときは文字が入った問題が多いので慣れておく必要がある。
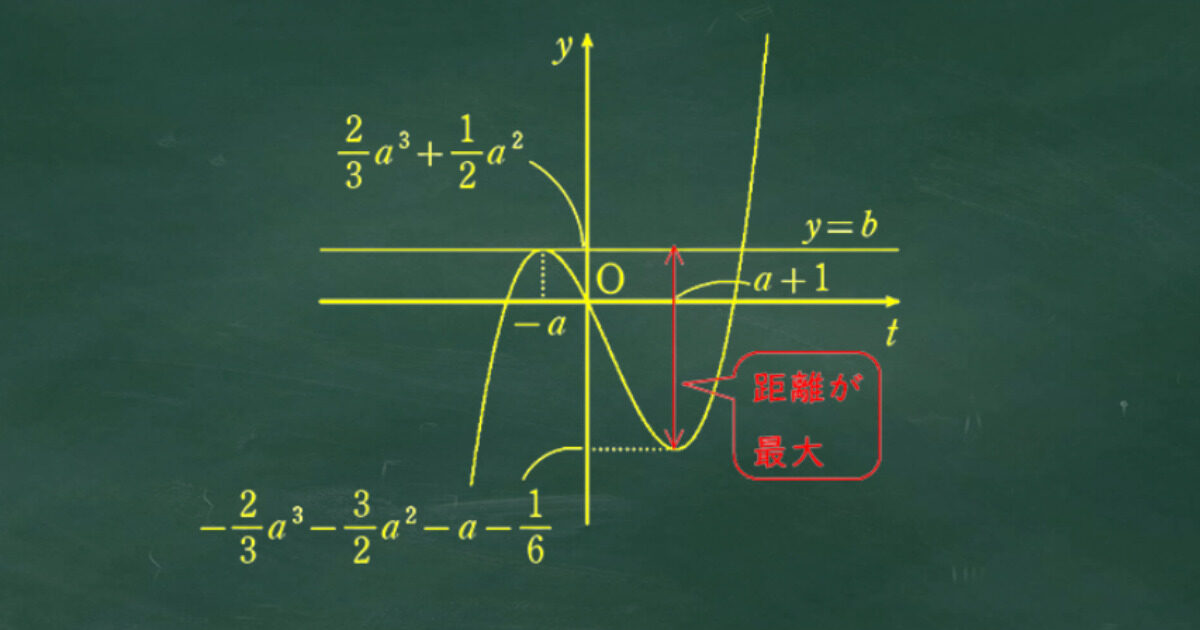
(1) の解法では連立した式から定数bを分離する、いわゆる定数分離問題とよばれるもので重要な解法となるのでしっかりマスターしてほしい。
解説
(1) の解説
f(x) と g(x) を連立して定数bを分離する。
関数 h(x) のグラフを微分することによって書き、図から共有点の個数が2つになるときのaとbの関係式を求める解法となる。

(2) の解説
共有点のx座標を求める問題。
文字の入った3次式の因数分解が必要となるのだが、解説にもある通り重解をもつことに注意すると因数分解をしやすい。

(3) の解説
絶対値が入っていることで問題が難しく見えると思うが、(1) のグラフを利用して考えると絶対値をすぐ外すことができる。
やはりこの問題もグラフから問題を理解する事になるので、しっかりグラフを書く練習が必要だ。

終わりに
冒頭にも書いたが、3次関数の問題は文字が入った形で出題されることが多い。
文字が入ると場合分けをする必要があることが多いが、この問題みたいに案外あっさりグラフまで到達できる問題もある。
見かけに騙されず、しっかり手を動かして、いけるところまで問題を進めてみることが大切だ。








コメント