参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2023横浜国立大大問4(理系)
問題

数学Ⅱの数列と数学Ⅲの極限の融合問題。
数列の漸化式の問題だがこれを解くことはできない。
数学的帰納法やはさみうちの原理をうまく用いて極限を求める。
解説
(1) の解説
まずは漸化式のいわゆる特性方程式を解く。
解が1つしかないことを証明する部分が少し大変だ。
2乗してルートを消しながら4次式の因数分解を行い、解を求める。

(2) の解説
この手の証明問題は数学的帰納法を用いることが多い。
様々な大学の過去問に触れながら練習してほしい問題。

(3) の解説
(2)がはさみうつ片方の誘導になっているのでもう片方を考えることになる。
(1)で求めた特性方程式の解を両辺から引くところがポイントだ。
このような無理数の入った漸化式は有理化を行えばよい。

終わりに
漸化式の問題から極限を求める数列の問題は頻出分野だ。
この問題のように、漸化式から数列が求められない問題の場合、解法にあるように誘導をうまく使いながら解くことになる。
その中で用いられるのが数学的帰納法とはさみうちの原理だ。
とにかく問題になれることがこの手の問題を完答できるようになるコツだ。







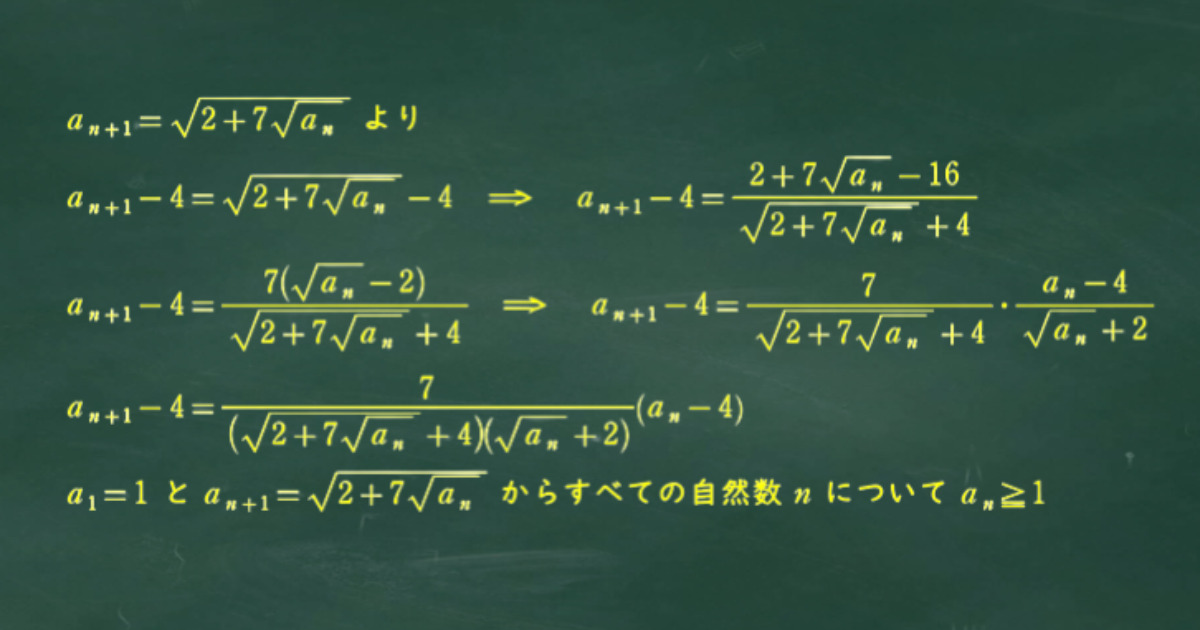


コメント