参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022北海道大大問3(理系)
問題

連立不等式における領域の問題。
(1) をヒントに (2) の領域を考える。
積分を用いて領域部分の面積を求め、微分を用いてその最小値を考えるのが定番だが、この解説では積分を行った後、微分を使わずに解説をする。
場合分けも細かく行うため、難易度がかなり高い問題だ。
解説
(1) の解説
問題文に自然対数の底 e があるので、対数を利用することは容易に判断できる。
この手の問題は、対数をとるときに底を何にするかが悩みどころだが、数学Ⅲ履修者はぜひ自然対数の底eを使ってほしい。

メインの関数の増減表からグラフの概形が書ける状態になったら、次にy=2との交点を考える。
その際、x=2はすぐ求まるが、x=4は思いつかない人もいるだろう。
これはグラフの概形からx=2以外にも交点があることに気づけば、あとはあたりを付けて探すしかない。
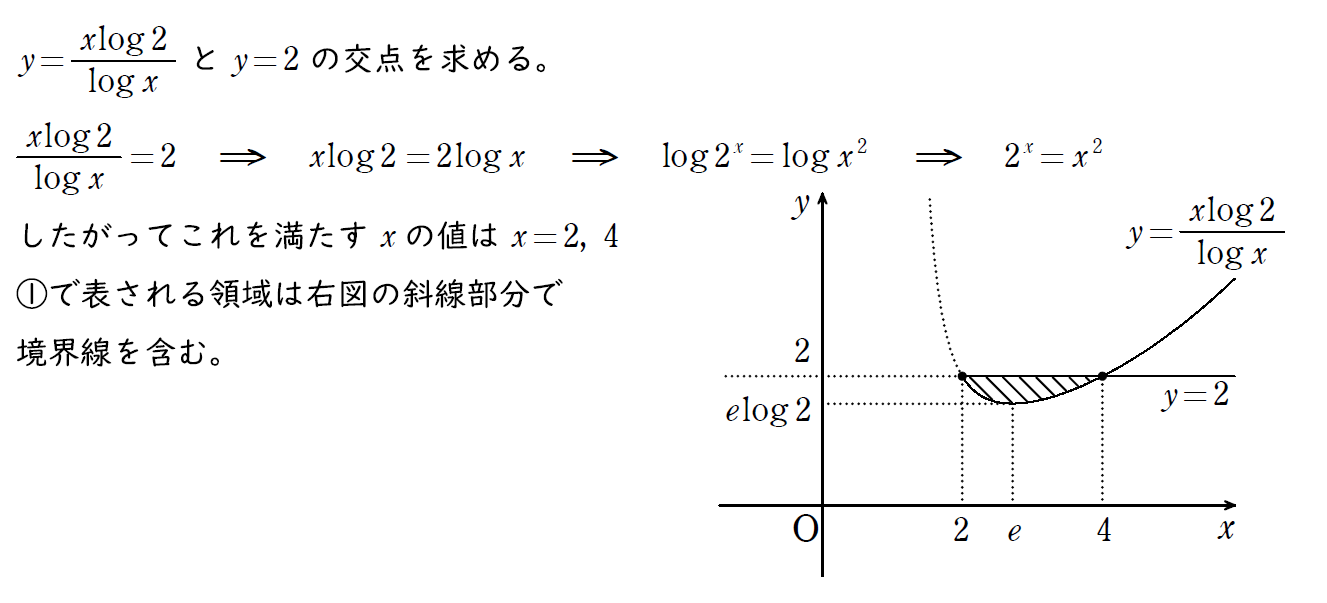
(2) の解説
まずは連立不等式の形を (1) をヒントに変形し、グラフを書きやすい状態にしておく。

a の値が変化することに伴い、囲まれる領域部分も変わるのでこれを丁寧に場合分けして考えていく。
直線 y=a が動くので a の範囲で以下のように場合分けを行う。
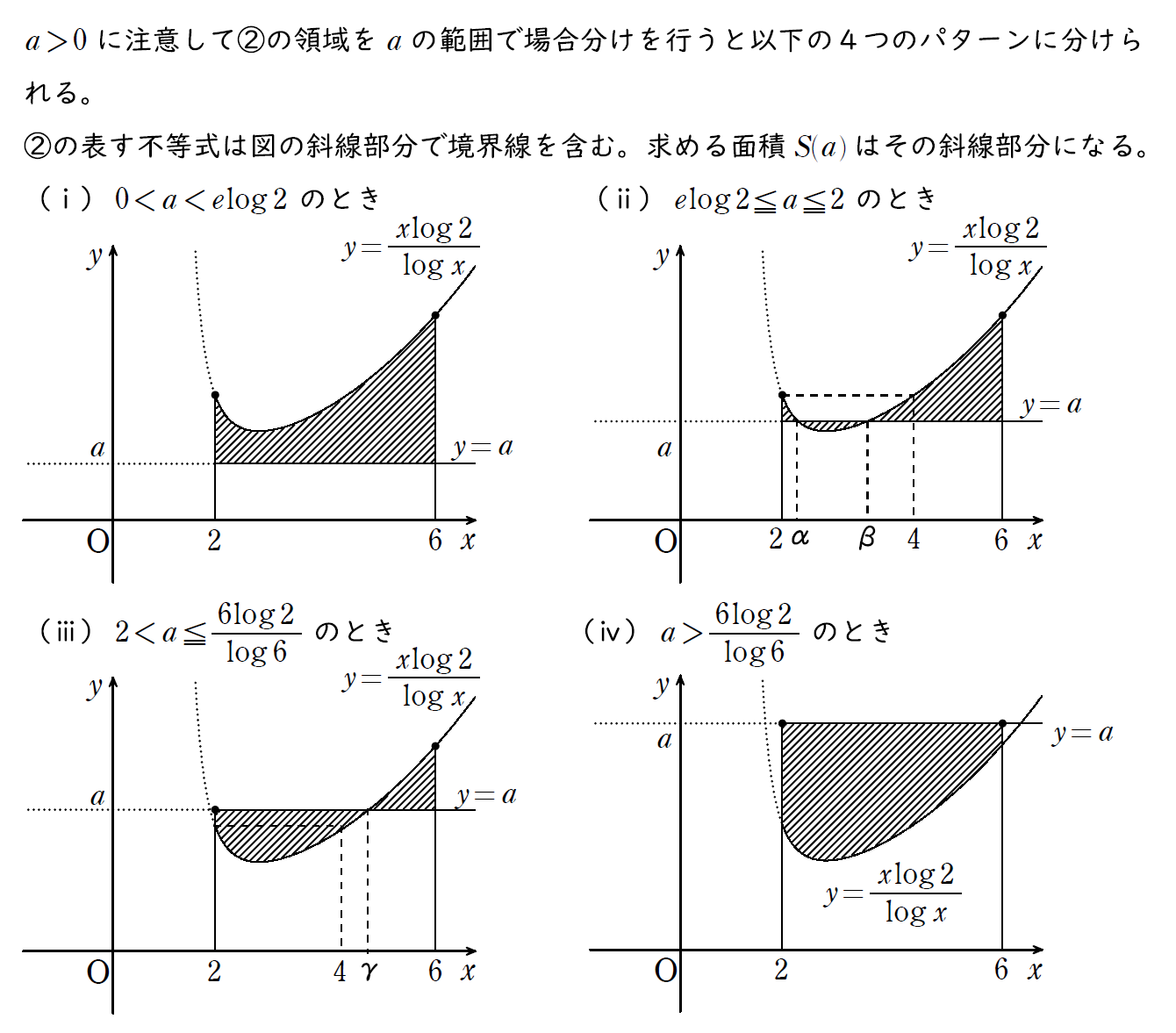
関数 f(x) の積分が厄介なうえに f(x) と g(x) の交点が求めにくいため、このあたりで挫折する受験生も多い。
実際の積分計算は行わず、原始関数を設定するとよい。
また、交点は文字を使って表す。

(ⅰ)の場合は曲線と直線が交わらないため2≦x≦6の範囲で積分すればよい。
積分後の S(a) の式は直線の式になるので、あとは傾きを調べるだけ。

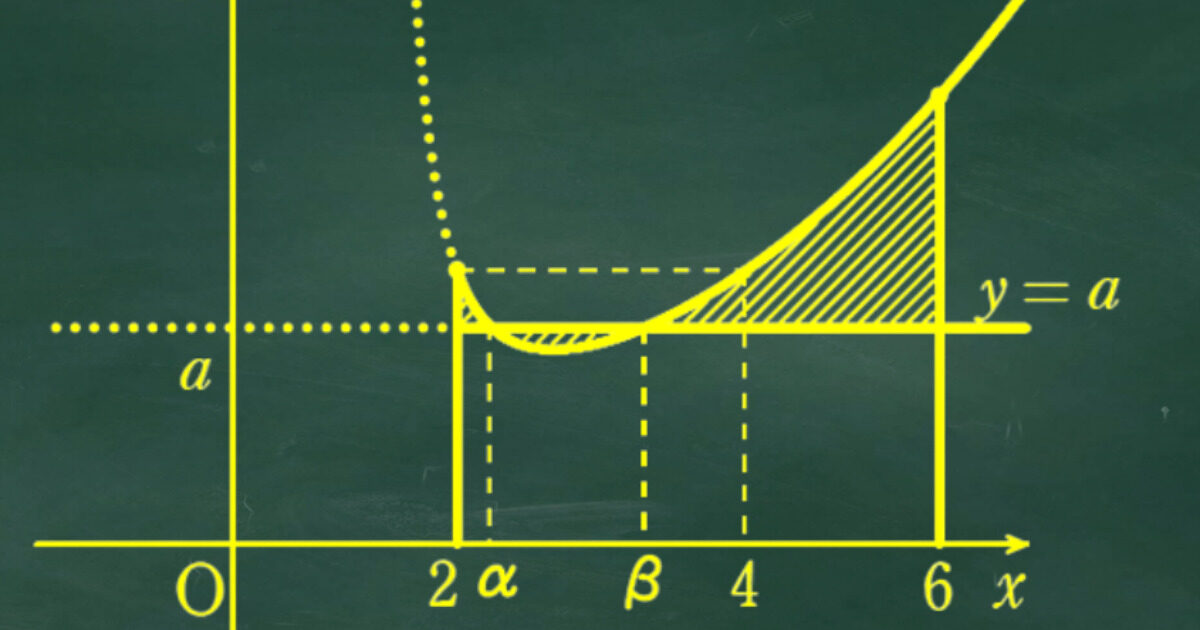
(ⅱ)は曲線と直線の交点を求めることが難しいので、交点をα、βと文字を使って置くことになる。
α、βはaの値によって変化するので変数として扱うことになるのだが、そうすると多変数による微分を行わなければならない。
ここではα、βを定数扱いにしてaの1次式、つまり直線として扱うことにより求め方を簡略化した解答を紹介する。

(ⅱ)と同様に曲線と直線の交点をγと文字でおく。γを固定して直線の傾きを調べ増減を考える。

これは(ⅰ)と同じパターン。
これも積分した式がaの1次式になるので直線の傾きを考えればよい。

終わりに
(1)をヒントにしても(2)は難易度が高い。
「場合分けを行い、積分をし微分をする」という一見ありがちな問題だが、積分そのものが難しく曲線と直線の交点も求まらない。
場合分けまで辿り着き、あとは積分をと考える受験生もここで手が止まってしまう。
今回の解説を読んで、この手の問題の攻略法をぜひマスターしてほしい。








コメント