参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022横浜国立大大問1(文系)
問題

数列の漸化式の問題。
よくありがちな典型的な漸化式の形と違うので、いろいろな角度から問題をとらえる必要がある。
(2) が解ければ (3) はスムーズに求めることができるので、計算ミスがないよう注意したい。
解説
(1) の解説
共通テストでもよく見かけるが、数列の規則を見つけるためにはまず、初項からいくつか項を並べてみることが漸化式を解く糸口になる。
この問題は誘導になっているが、この誘導がなくてもまずは並べてみる習慣を付けることも数列の問題では大切だ。

(2) の解説
この漸化式は特殊な解法があるわけではなく、教科書でも取り扱っている一般項を推定して数学的帰納法を用いて正しいことを証明する問題だ。
解法が思いつかないときにはこの推定して帰納法という解答は使えるので覚えておきたい。
r=1のときだけ特別な形になることに注意しなければならない。
r=1とそれ以外に場合分けして解答を作ろう。

ここからは教科書などでもよくある解答で、問題文の漸化式と自分で推定した一般項を連立してn=k+1が正しいことを導くことになる。
数字が少し複雑に見えるが、解説を読んで流れをしっかりつかんでほしい。

(3) の解説
(2) で求めた一般項を使って和を求める問題。
(2) の式が間違っていなければ完答できるのでしっかり答が合うまで見直しをする必要がある。
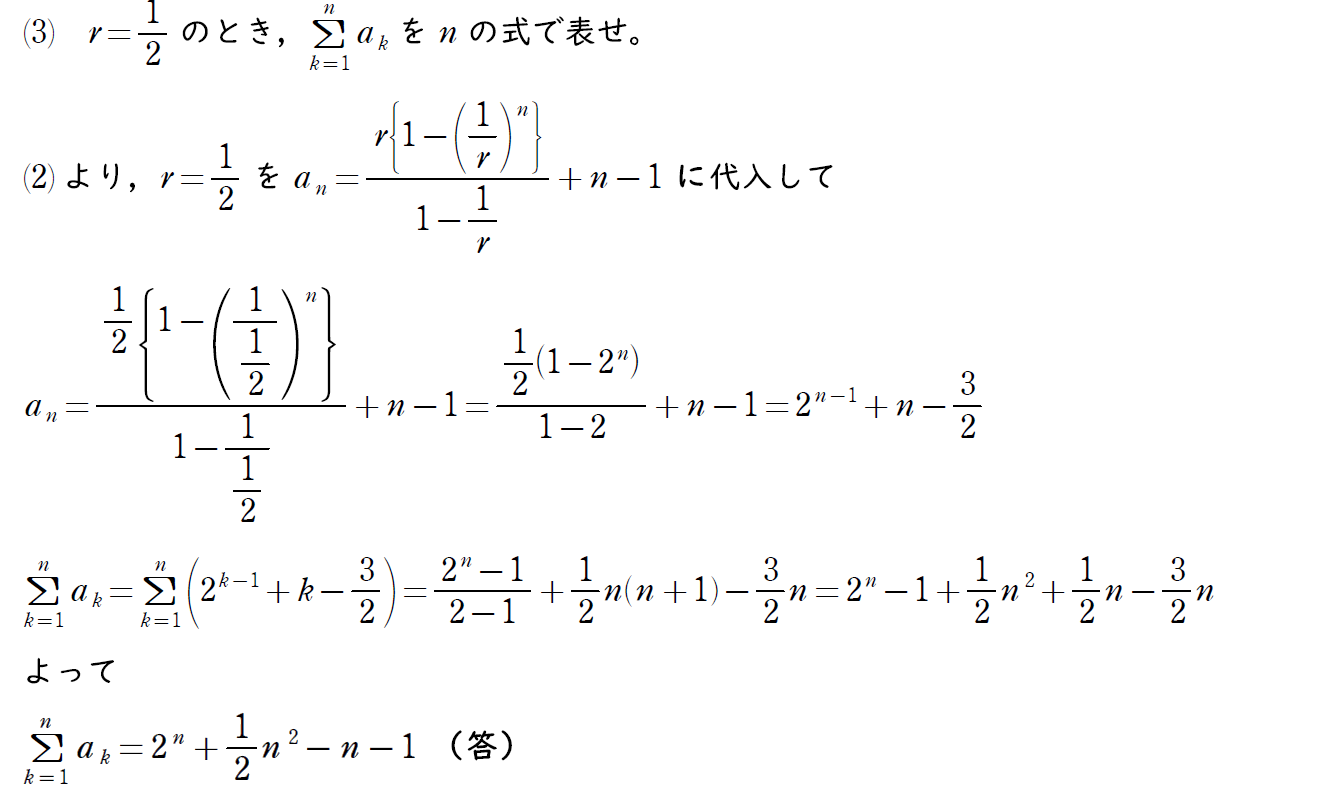
終わりに
数列の勉強をしていると漸化式の問題は多数触れる機会があると思う。
漸化式の問題は解法をパターン化して解き切る問題も多いが、この問題のように推定して数学的帰納法で処理する問題もいくつか見かけるので練習をしておこう。
練習をしっかりしていれば難易度的には高くないので完答できる問題だ。










コメント