参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022千葉大大問5
問題


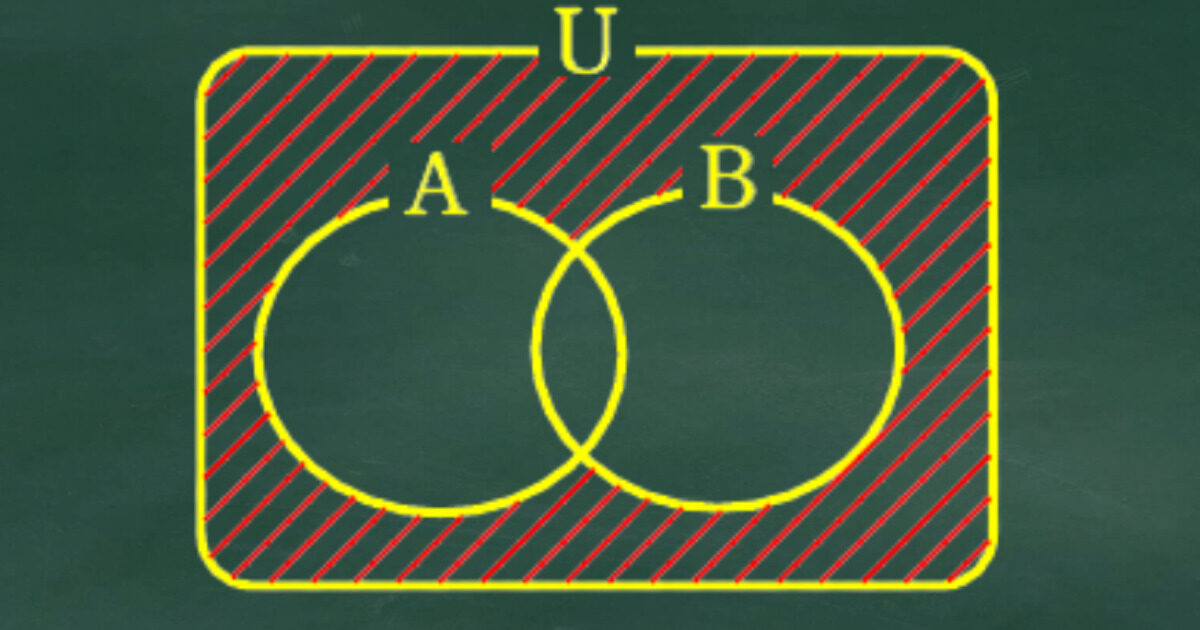
この問題は確率ね。でも「2や3で割り切れない」は集合の話かしら?

「n個のサイコロを投げる」が難しい所かな。問題は複雑ではなさそうだから具体化する必要はなさそうだね。
この問題で大事なことは次の2つ
- 確率は問題文をしっかり理解して説明しやすいい言い方や式に変えてみよう
- 小問に分かれている確率や集合の問題は誘導されている場合が多い
解説
「n個のサイコロを同時に投げる」だけ見ると複雑そうだけど、求めるのが「出た目の積」なので意外とあっさり解けるよ。
(1) の解説

「2でも3でも割り切れない」みたいに「~でない」のときは余事象で考えた方がいいんでしょ?

確かに「~でない」のときは余事象を使うことが多いけどこの問題は使わない方がいいよ
なぜここでは余事象を使わない方がいいのかを説明するね。

この問題は「2でも3でも割り切れない」と2つの集合の否定なので少し複雑だよ。

これは余事象の落とし穴なので覚えておこう!
M はn個のサイコロの出た目の積なので1つでも2の倍数か3の倍数の目が出ると2か3で割り切れてしまうよ。
2の倍数2,4,6の目と3の倍数3,6の目が1つも出ない場合を考えればいいよね。だから解答は次のようになるよ。

(2) の解説
この問題も余事象を使わない方がいいよ。
理由は (1) と同じで「かつ」が入っているからだね。

(1),(2)は意外とあっさり求めることができたね。次の(3) はどうかな?
(3) の解説

(3) の問題は(2)と似てるから同じ解き方で解けるかな?

この問題は「4で割り切れる」が難しい原因だよ。
(2) の「2で割り切れる」は1回でも2が出ればいいんだけど、「4で割り切れる」はいろんなパターンが考えられるから難しいんだね。
この問題は (1)、(2) が誘導になっていてこれを使えば解けるんだけど、どう使えばいいかが分かりにくいよね。
「4で割り切れる」が難しいのでまずは「3で割り切れない」から考えてみよう。

↑ この中から4で割り切れないものを取り除くよ

↑ これを取り除くよ

↑ これも取り除くよ

終わりに
確率は問題文を理解するのが難しいよね。
「~でない」は余事象を使うと間違いの原因になる事にも注意が必要だったね。複雑な問題のときは余事象を使わないほうが無難だね。
あとは問題の前半が誘導になってることに気づけるのも大事だよ。








コメント