参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022千葉大大問6
問題


今回はベクトルの問題ね。空間ベクトルは難しそう。

空間ベクトルは図を書くのが大変だけどこの問題は図無しでも行けると思うよ。
この問題で大事なことは次の3つ
- ベクトルの直行条件「内積が0」を使う
- 最小値を求めるには「平方完成」を使う
解説
空間ベクトルの問題はできれば図を書いた方がいいんだけど、難易度が高いよね。そういう時は「略図」などで代用するといいよ。
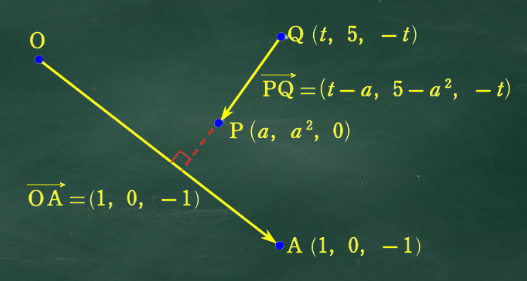
(1) の解説

この問題は「垂直」がキーワードね。

ベクトルで「直交する」が出てきたら「内積が0」を使うよ。
内積の公式
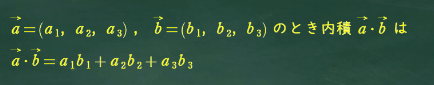
「直線上にある」とか「〜を通る」のときはその方程式に代入するんだよね。ベクトルの場合は「成分」に代入することになるよ

(2) の解説

ベクトルの大きさを求めるところまではそんなに難しくないかな

じゃあとりあえずそこまで解答を作ってみよう

問題はここからね。「最小値」を求めるにはどう考えたらいいのかしら?

「最小値」の問題はいろんな分野で出てくるよね。

「最小値」の問題はとりあえず次の3つの方法を考えるといいよ。
- 平方完成をする
- 相加平均・相乗平均の関係を使う
- 微分してグラフを書いて考える
この問題では1番の「平方完成をする」を使うよ。
平方完成をするとなぜ最小値が求まるかは以下の通り
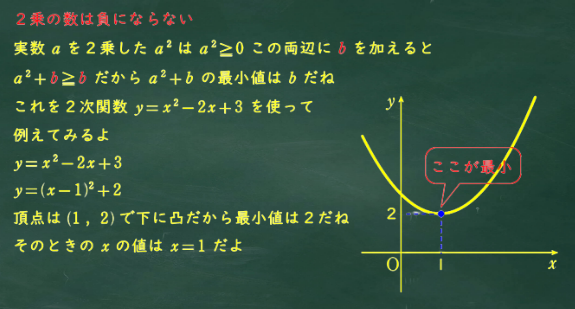

平方完成はわかったけどこの問題は文字が2種類あるけどどうするの?

文字が2種類あってもどちらかについて平方完成すれば問題ないよ
この問題では r と s の2種類があるけど r は2次式、s は4次式の違いがあるね。
平方完成といえば2次式が多いから s について平方完成をやってみるよ

でもこの問題は大きさの式だからルートがついてるけど?

最小値の問題にはこのルートは影響しないんだ。
この後の解答のようにルートの中身だけを取り出して考えるといいよ

とりあえず s についての平方完成はできたね。この後はどうするの?
まだ r の4次式が残ってるね。これも平方完成してみよう。
わかりにくければ解説のように r 2を別の文字に置き換えれば2次式として考えられるよ。

終わりに
ベクトルは図のイメージが難しいんだったね。
略図でいいので図を書く練習をたくさんしよう。
最小値の問題はよく見かけるのでまずはどのパターンに当てはまる問題か見極めよう。








コメント