参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2023北海道大大問4(文系)
問題

数学Ⅱの微分積分の問題。
前半は共通接線となるときの接点を微分を使って求める。
後半は囲まれる部分の面積を積分を用いて求める。
解説
(1) の解説
放物線上にある接点を文字でおく。
その接点における接線を放物線と円についてそれぞれ求める。
それぞれの接線が一致するので係数を比較してqの値と接点を求める。

(2) の解説
この問題は (1) で求めたqと接点の値を用いる。
(1) ができていないと (2) へは進めない。
理系選択者は数学Ⅲの積分を使えばやや簡単に面積を求められるが、数学Ⅱまでの範囲だと扇形の面積を取り除く考え方が必要だ。

後半は扇形の面積を求め、積分を使って求めた曲線で囲まれる部分の面積から引くことによって求めることができる。

終わりに
共通テスト(旧センター試験)でも出題されたことのある円と放物線で囲まれた部分の面積を求める問題。
慣れていないと方針が立たないので演習をしっかり行っておきたい。
理系選択者は数Ⅲの積分を用いて考えてもよい。







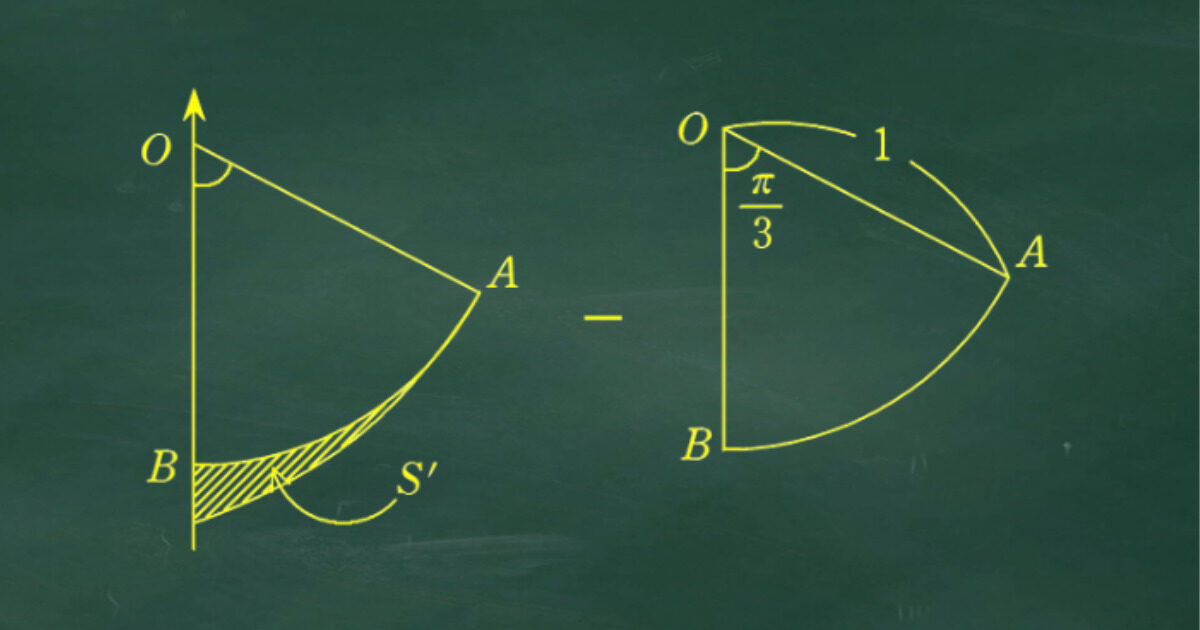


コメント