【2022】北海道大学入試問題数学大問２(理系）をとことんわかりやすく動画を使わずに解説します

参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか？

YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。

この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。

2022北海道大大問２（理系）

問題

問題文をみるとベクトルの問題に見えるが大部分が数列の問題。

後半は少し難解な漸化式を解くことになるので、説明の部分が長くなるが頑張って理解してほしい。

解説

(1) の解説

与えられた座標とベクトル Q_nQ_n＋１ の成分を用いて求める。始点を原点 O にすることがポイントだ。

(2) の解説

(1) で求めた漸化式を利用して ｘ_n を求める。

③ の式は３項間漸化式なのでまずはその求め方を復習しておこう。

文字 a が入っているので複雑そうに見えるが、特性方程式を用いて漸化式を変形すると、教科書レベルの問題となる。

解説にもある通り、a の条件はきちんと説明しよう。

(3) の解説

(2) と同じ３項間漸化式の問題だが、難易度が格段に上がる。④の式にある a^-n が厄介だ。

この手の漸化式の問題は教科書では見かけることがないので、受験用問題集や大学の過去問集なので練習してほしい。

ここからの解説は長くなるが、きちんと読み込んで理解できるよう頑張ろう。

(2) の漸化式に似ているため、それをヒントに次のように変形することに気づきたい。

２項間の漸化式に置き換えられるように以下の手順で変形していく。

この漸化式には文字が入っているため難しく見えるが、内容は教科書にある標準的な漸化式の問題。

まずはこの漸化式の変形方法を復習しておこう。

特性方程式を使っての変形

２つ目の式も同様に変形して連立を行う。

手順は全く同じで特性方程式を用いて変形。w_n の初項を求めるのに少し時間がかかる。

⑩ と ⑫ の２つの式から y_n+1 を消去する。

長い計算も大詰めなのでミスをしないように注意しよう。

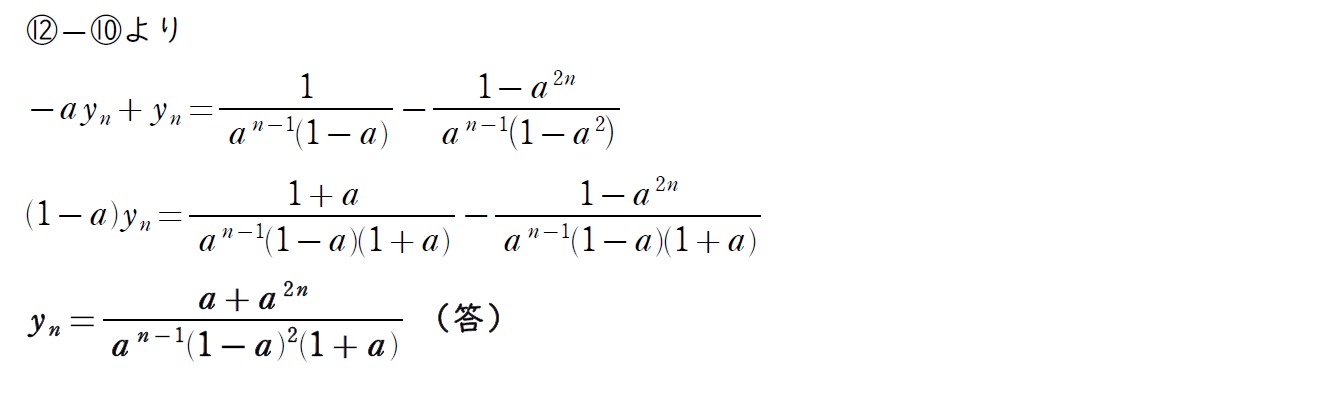
終わりに

数列の漸化式は入試で数多く出題されている。

教科書や参考書などで取り上げられる漸化式は定番のものが多く、解法に定石がある。

そんな中で、この問題の特に (3) の漸化式は初見で解くには難しい。

どの問題集にもこのタイプの漸化式があるわけではないので、このような過去問を用いて経験を積み重ねるのが一番の対策となると思うので頑張ってほしい。