参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2023令和5年度大学入学共通テスト数学1A大問2
[1] (1)問題
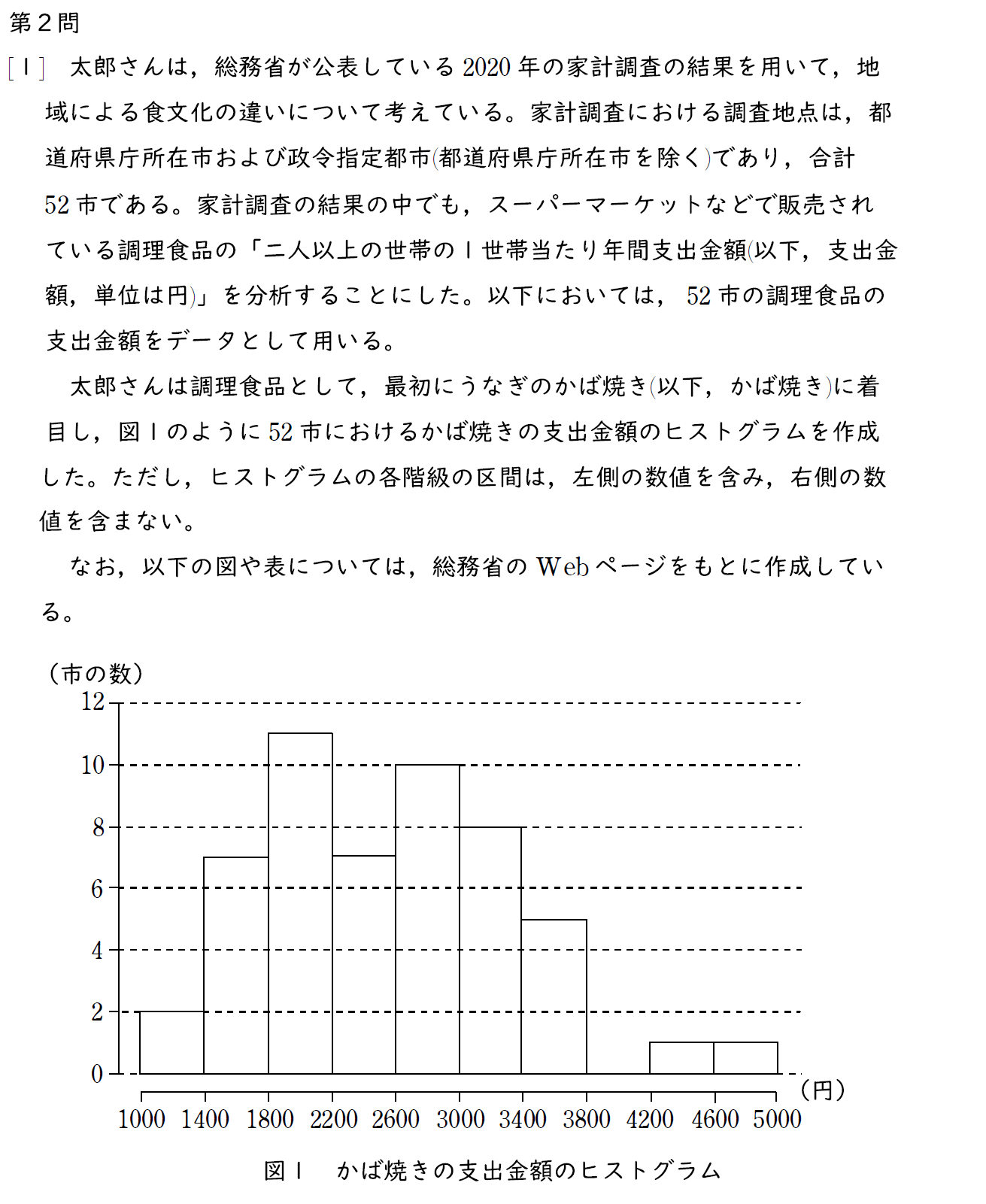

[1] (1)解説
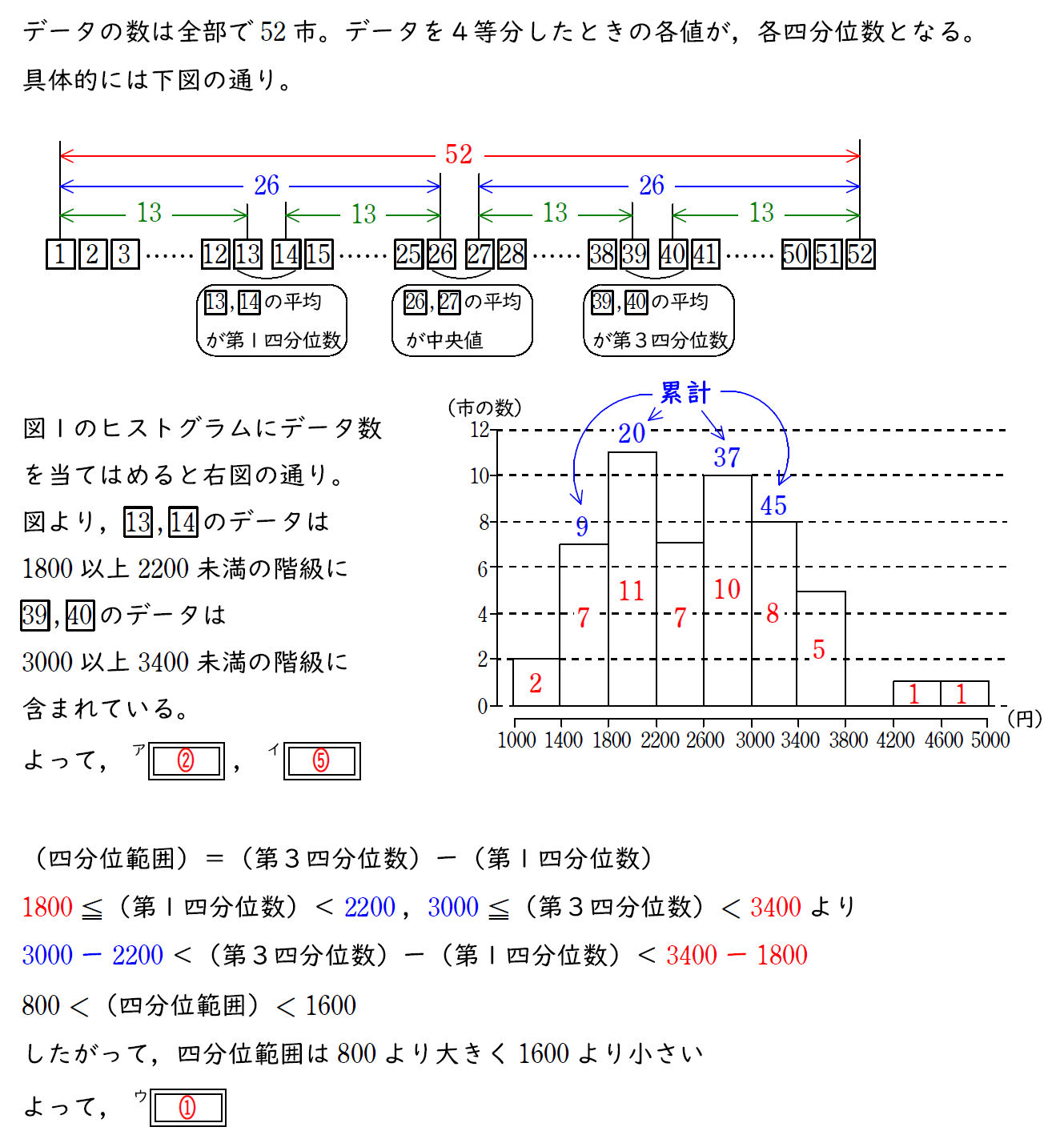
52 あるデータを四等分し、各四分位数を求める。
後はヒストグラムの左から累計していき、四分位数がある階級を探す。
四分位範囲は「(第3四分位数) — (第1四分位数)」だが、階級幅があるのでそれぞれ (最大数) ー (最小数) および (最小数) ー (最大数) で求めることになる。
[1] (2)(ⅰ)問題
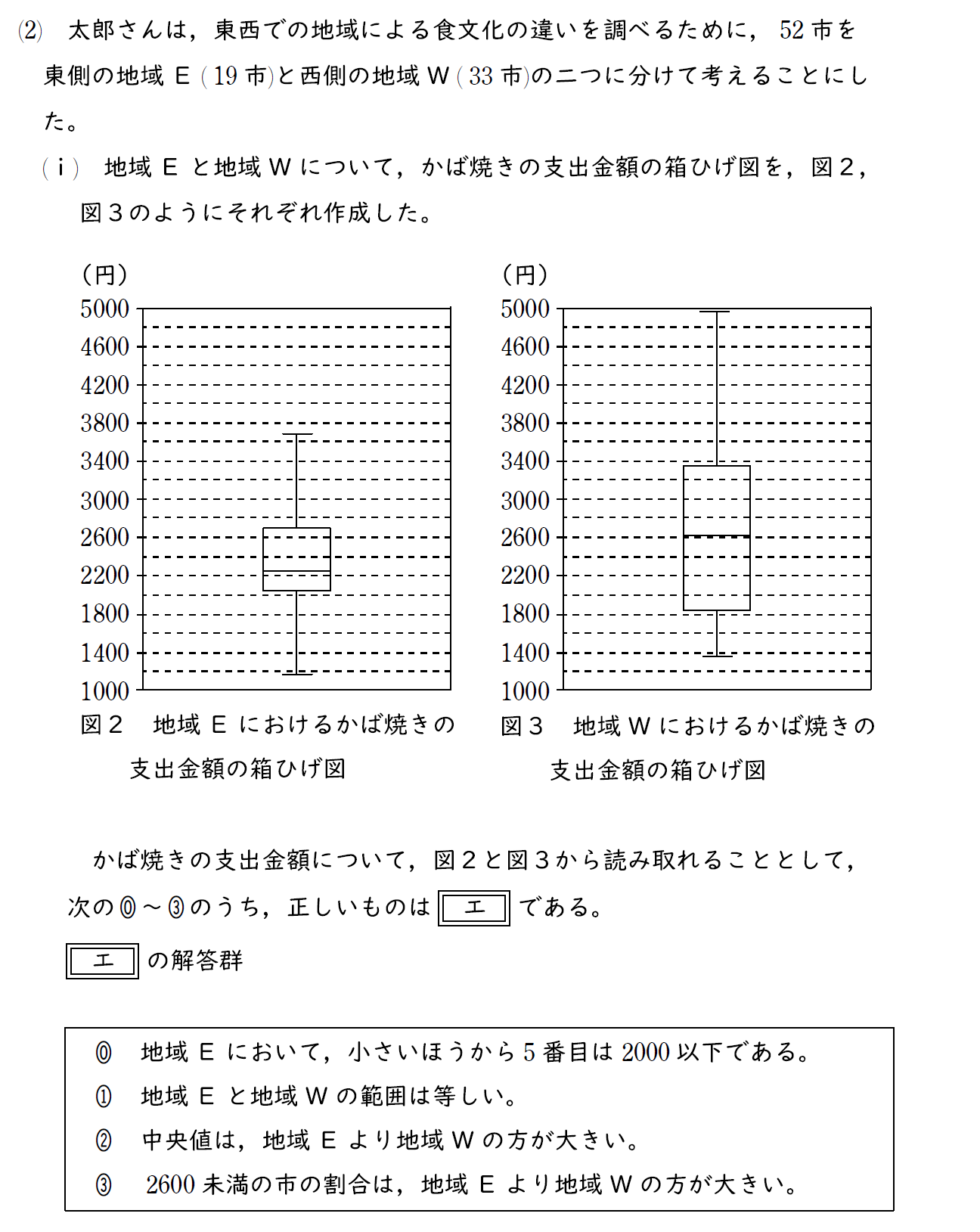
[1] (2)(ⅰ)解説
四分位数と最大値および最小値の位置を箱ひげ図から読み取る問題。
演習の段階では答えが見つかった時点で終わりにせず、すべての選択肢を検証しておくと力が付くので最後まで解き切ろう。

[1] (2)(ⅱ)問題

[1] (2)(ⅱ)解説
分散を求める式の説明。
公式通りに文章を当てはめれば選択肢がみつかる。
難易度は低く基本的な問題。

[1] (3)問題
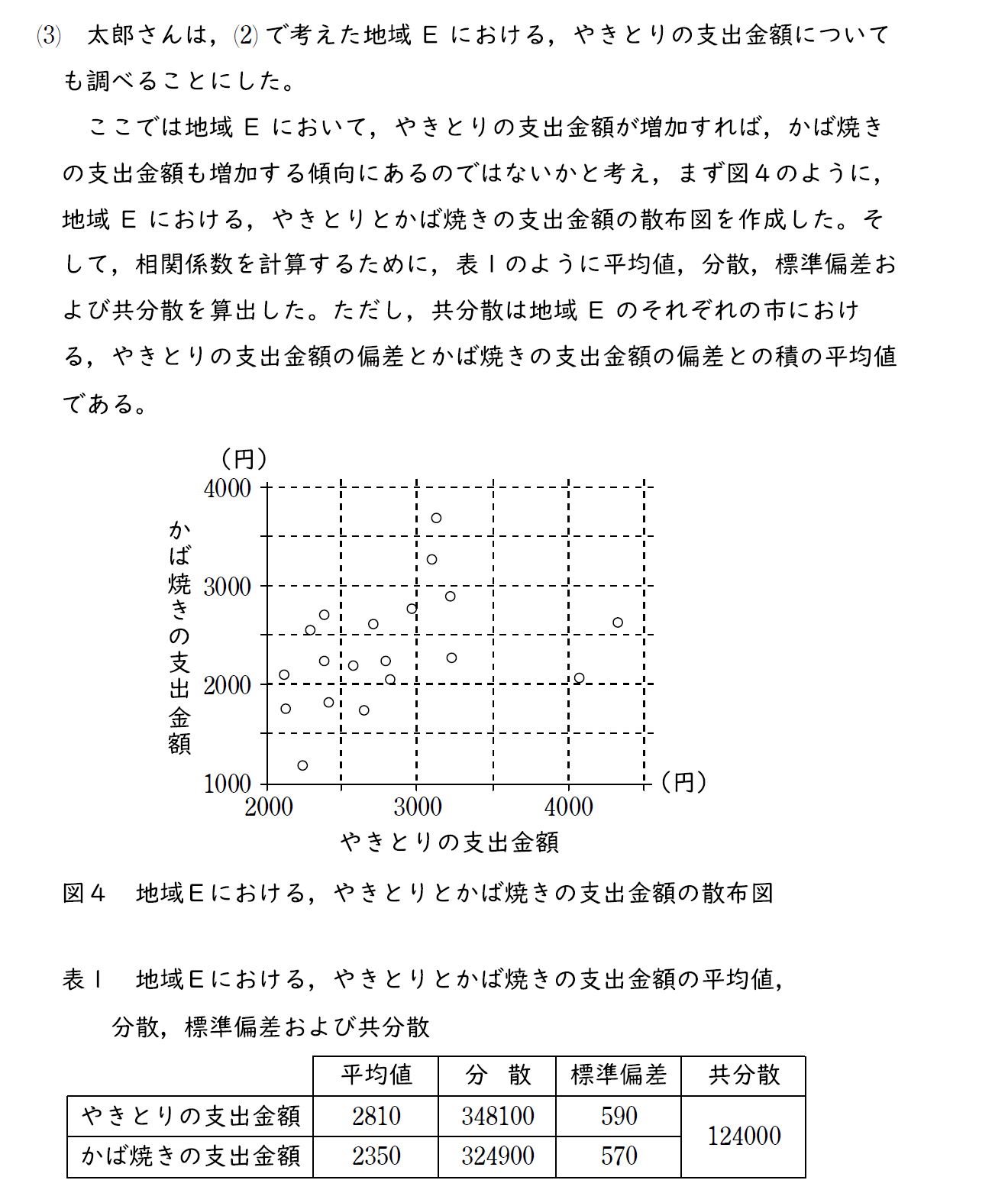

[1] (3)解説
相関係数の公式に表の数を当てはめる。
数字が多少大きいがルートも入っていないので、難易度はそんなに高くない。

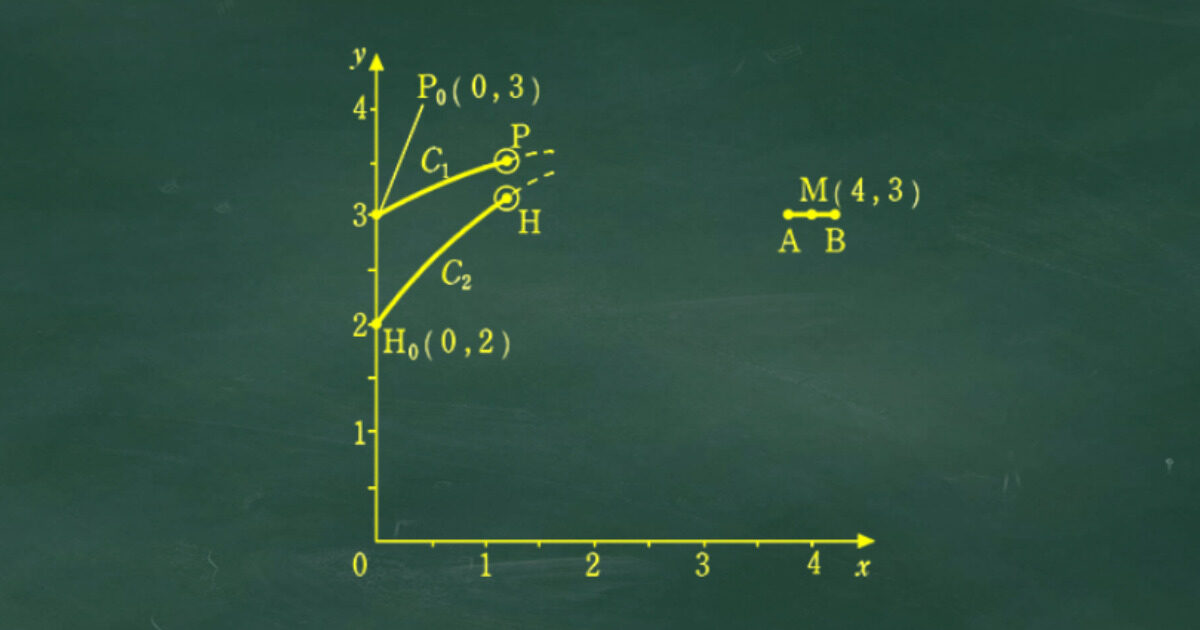
[2] (1)問題
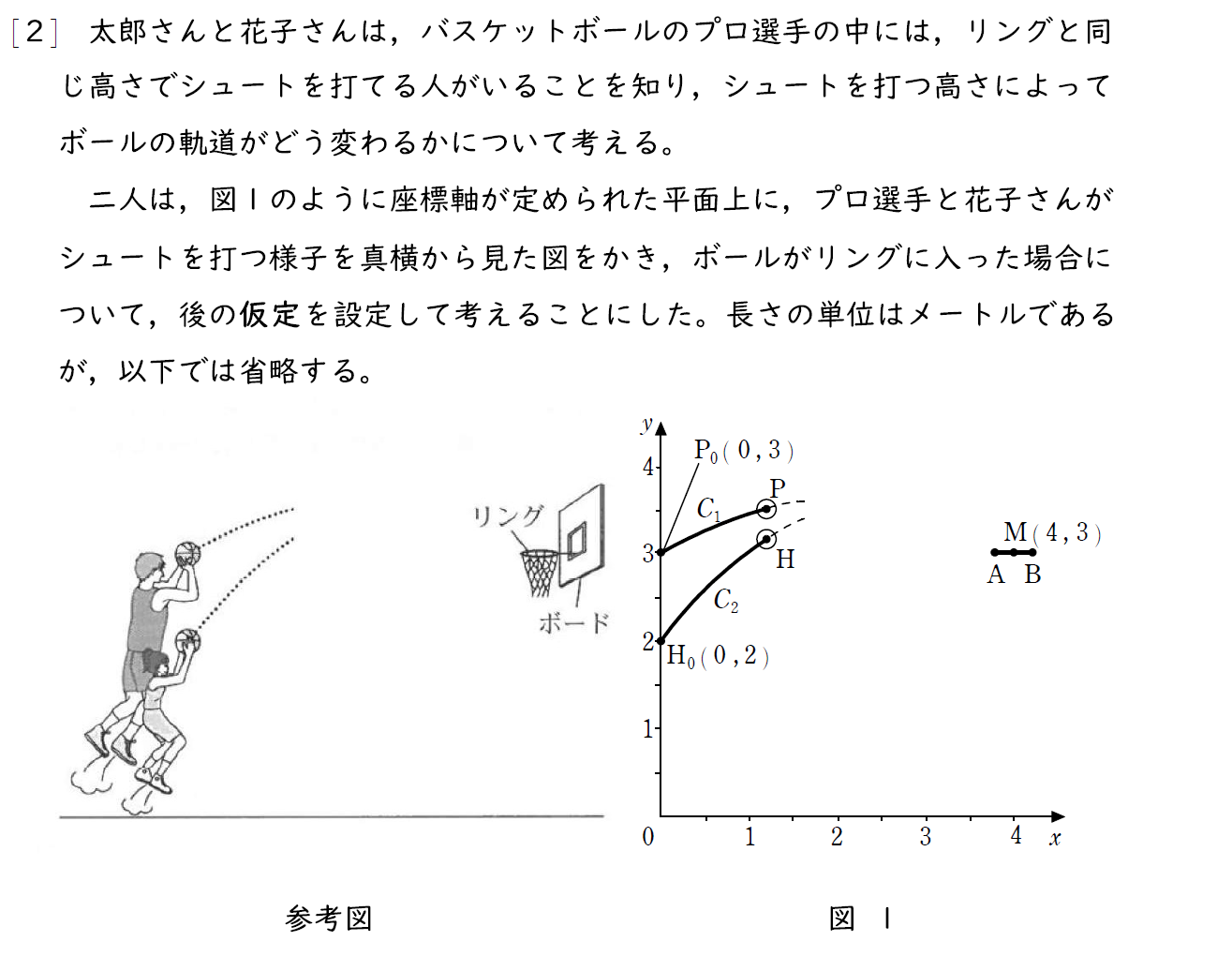

[2] (1)解説
イラストを見ると一見難しそうに見えるが、要は通る点を2つ与えられたときの2次方程式の決定の問題。
これも丁寧に誘導してあるので難易度は高くない。

[2] (1)問題のつづき

[2] (1)解説のつづき
問題文の仮定の中に「ボールが最も高くなるときの地上の位置」の説明があるので、その通りに計算を行う。
これも誘導が丁寧だ。

[2] (2)問題
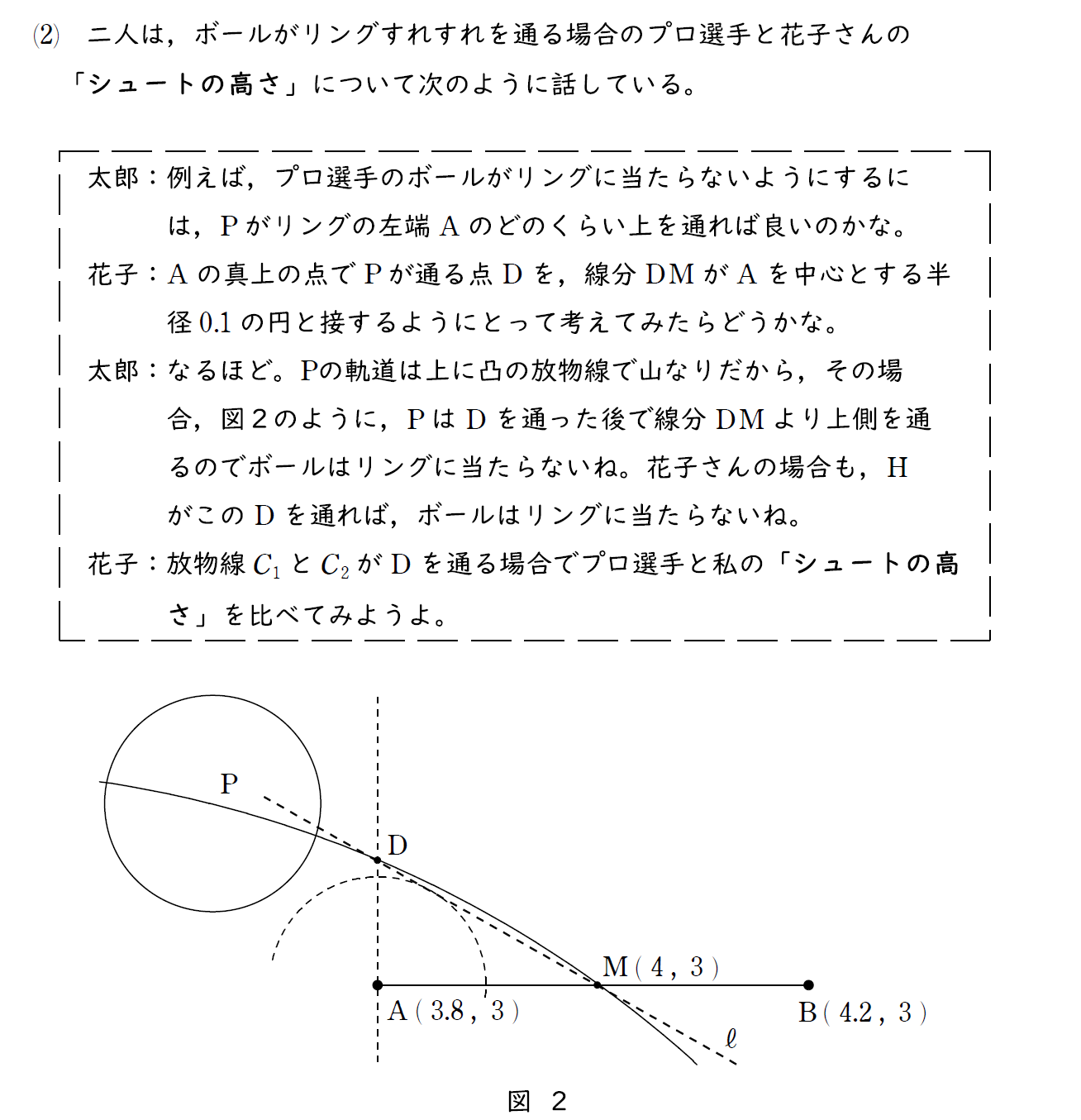

[2] (2)解説
2次関数の通る点 D を与えられているので、(1) で作った2次関数に代入してaを求める問題。
点 D が小数と分数、さらにルートが入った座標になるので大変そうに見えるが、丁寧に計算をしていけばたどり着く。
普段から計算練習をしっかりやっておこう。

終わりに
今年の大問2はデータの分析が前半で2次関数が後半という配置になっていた(例年は逆)。
データ分析は時間がかかるため、時間配分に苦労する受験生も多いが今年は難易度もあまり高くなく後半が時間不足になった者も少なかっただろう。
最近の共通テストの特徴である問題文の長さとイラスト入りの問題によって、解釈するのが難しく感じてしまう。
逆に計算内容も含めて問題のレベルはセンター試験時代より低いのでこのような出題形式になれる演習をすることが一番の対策となるだろう。







コメント