参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2023令和5年度大学入学共通テスト数学1A大問3
問題

(1)問題
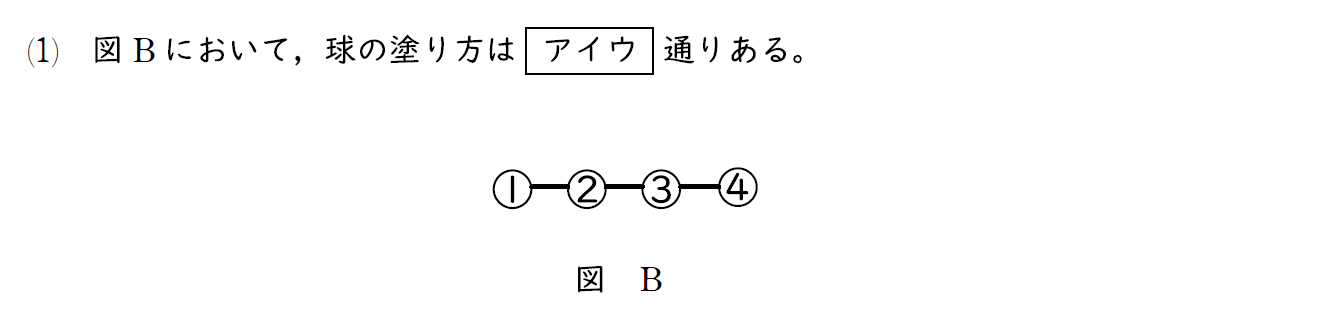
(1)解説
隣合う場所が同色にならないような塗り分けの問題は問題集でもよく見かける。
この問題のように (1) から順に丁寧に誘導されていると、非常に取り組みやすい。
球1から順に塗れる色を考えていけばよい。

(2)問題
これも球1から順に塗れる色の数を考えていく。
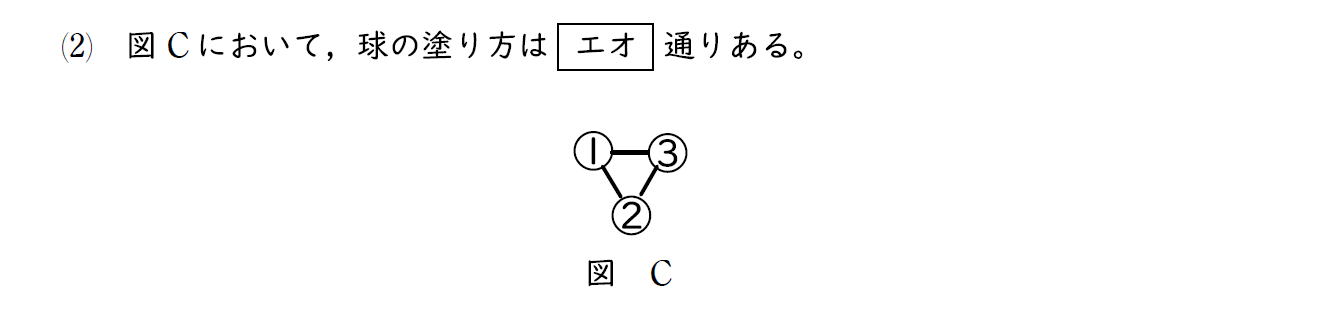
(2)解説

(3)問題
同じ色を2回使う指定があるので、まずは2回使う赤で塗る場所を選ぶ。
ただし、同じ色は隣合わないことに注意する。
残りの2か所は赤以外どの色でもよい。
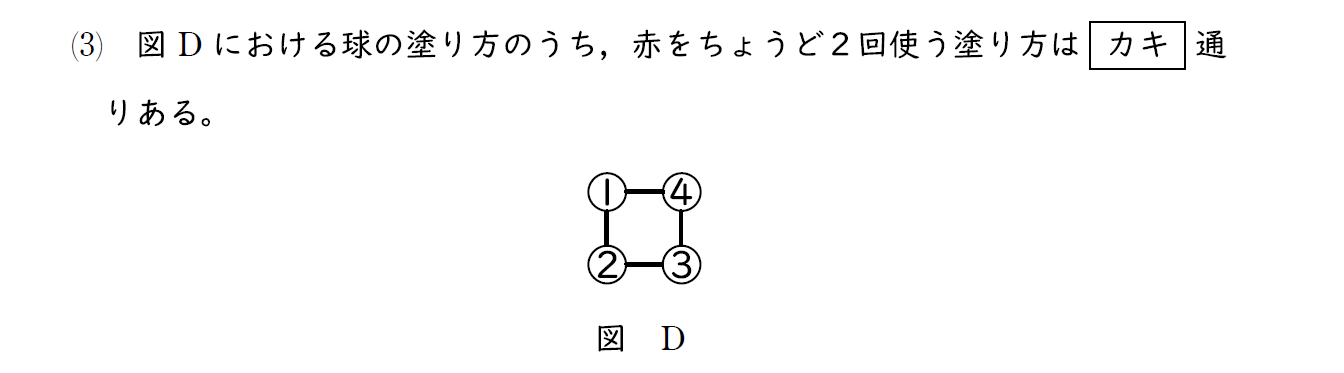
(3)解説

(4)問題
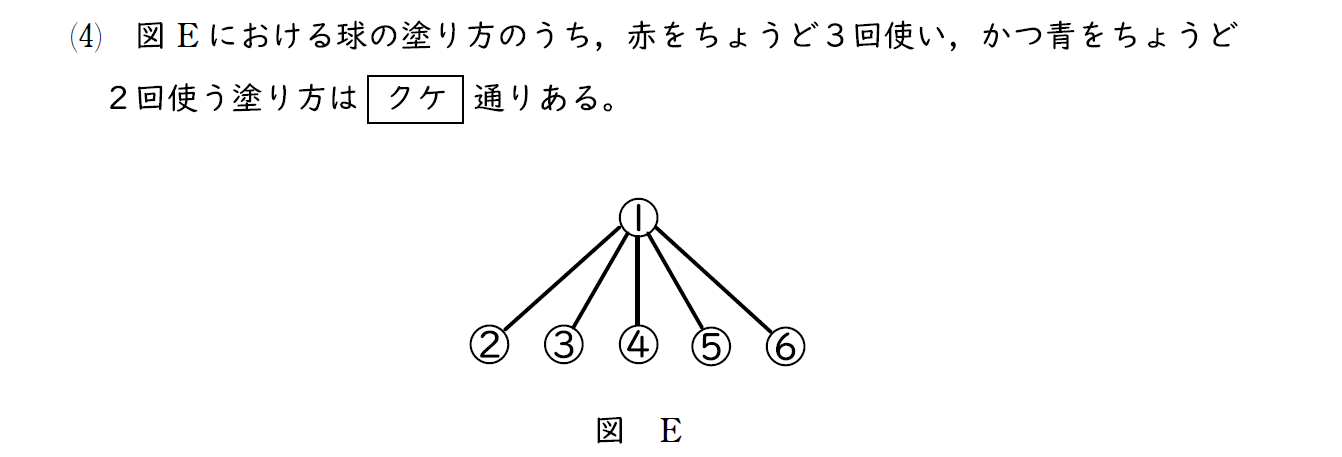
(4)解説
一見複雑そうに見えるが、球1には赤も青も塗ることができない。
よって,残りの5つの球から赤で塗る球を3つ選べばよいことになる。

(5)問題
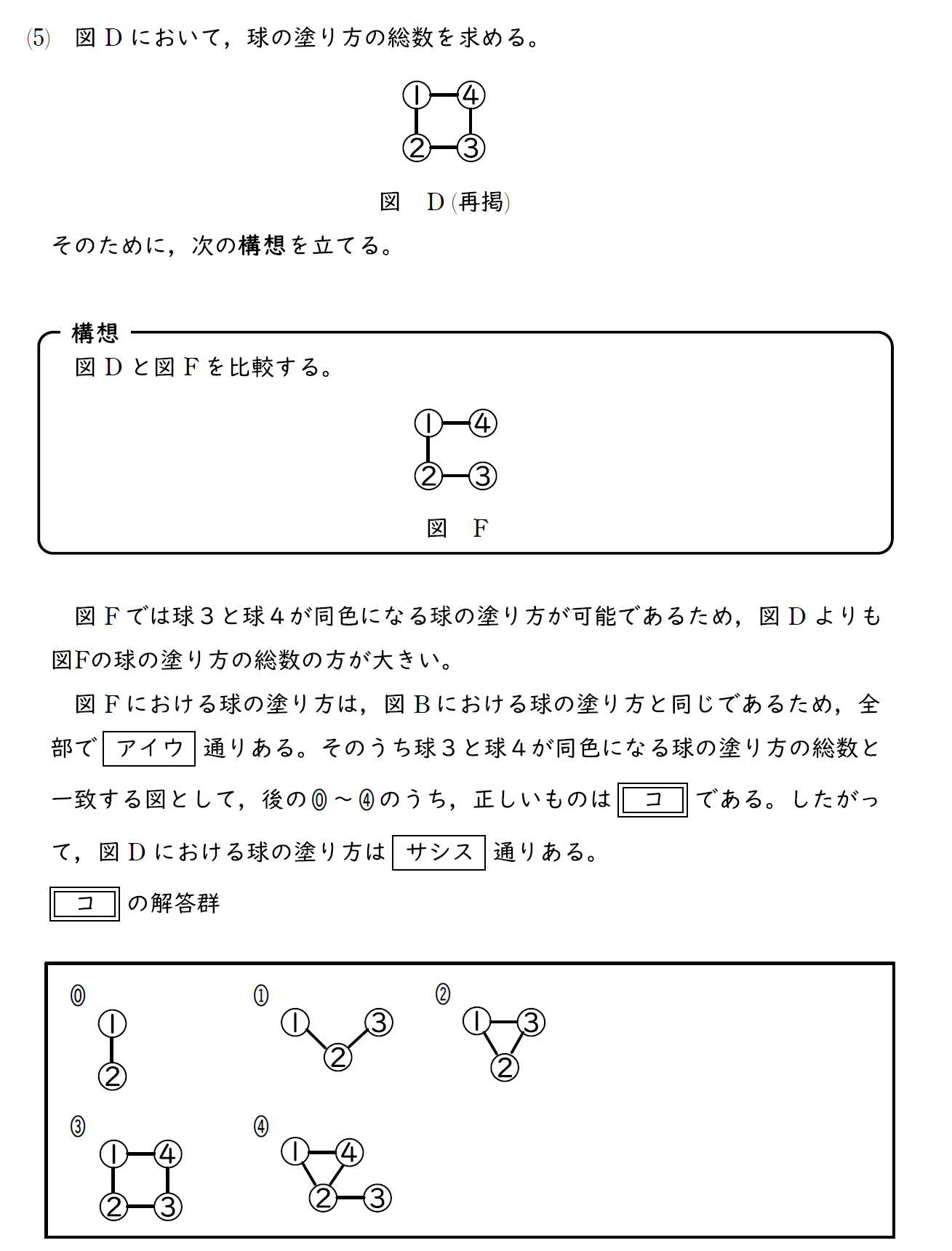
(5)解説
この問題が大問3の中で唯一難易度が高く複雑なので、詳細な解説を以下に掲示した。
ただし、誘導が丁寧なのでこの指示通りに計算していくとしかっり求めることができるはずだ。
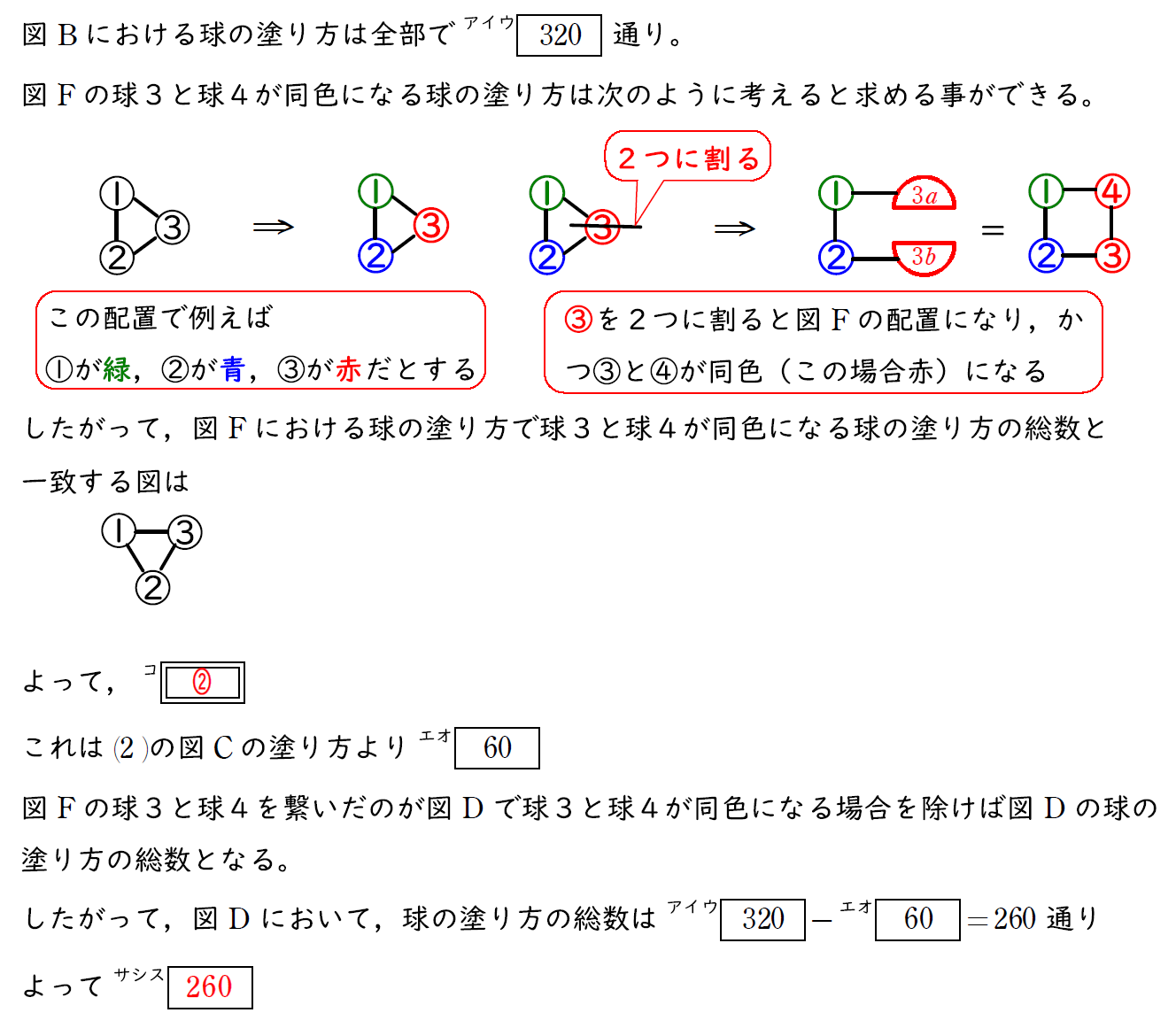
(6)問題
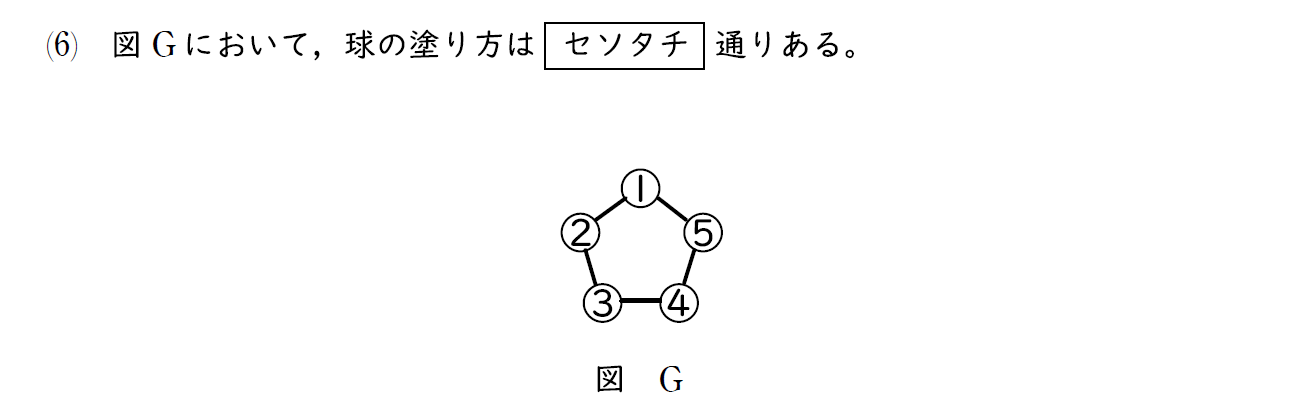
(6)解説
(5) の考え方がそのまま使える。
単純に球が1つ増えただけで計算方法は変わらない。
円順列の考え方も使えるが、ここは誘導を利用して時間をかけずに完答を目指そう。
終わりに
ほかの大問にも言えることだが、今年の共通テストはとにかく誘導が丁寧に作られている。
その反面、説明文が長く理解力を試されている問題となっていて、今後もこの傾向が続くものと思われる。
数学ではあまりなかったこの読解力・問題の把握力を身に付けていくことが今後は必要になっていくだろう。









コメント
(2)ですが、5・4・3÷3のように、円順列で考えると間違いになるのはなぜですか?
この問題は、なぜ円順列で考えるといけないのでしょうか?円順列で考えてはいけない理由を教えてください。
コメントありがとうございます。
質問に対する回答は以下の通りです。
「なぜ円順列で考えると間違えなのかというと、円形の3つの場所に1,2,3の番号が振ってあるからです。番号があると円形に並べてあっても直線に並べてあっても区別するので普通の順列として扱い、この番号がなければ3つの場所に区別するものがないので円順列として考えることになります。」
この回答で大丈夫でしょうか?さらに不明な場合は遠慮なくご質問ください。
教えていただきありがとうございます。
>番号があると円形に並べてあっても直線に並べてあっても区別するので普通の順列として扱い、この番号がなければ3つの場所に区別するものがないので円順列として考えることになります。
なるほど、番号がポイントでしたか。私は円形なら全て円順列だと思っていたのですが、ということは、番号があるイスを円形に並べるなども、普通の順列として扱わないといけないわけですか?
「番号がある場合は円順列は使えない」事は、暗黙の了解というか、暗記しておかないとダメなんでしょうか?
また、どういうときに円順列を使えて、どういうときに使えない条件とかあるのでしょうか?
とても素晴らしい質問をしていただいてありがとうございます。
以下に回答させていただきます。
円順列の考え方は順列では区別するものを円状にすると区別がつかないために用いられる公式です。例えば
-1-2-3-の「-」を紐だと思って輪っかを作ってみてください。すると
-3-1-2-と-2-3-1-も番号が同じ順番の輪っかになります(時計回りに1,2,3の順の輪になる)。
でも順列では(「-」の紐をなくすと)123と312と231は区別することになります。
円順列の場所に番号が振ってあると紐のついた上記の3つも区別することになります。例えばその場所にA,B,Cと名前を付けると
-1A-2B-3C-と-3A-1B-2C-となるからです。
最後にどういうときに使えるかですが、円状の場所に番号があったりせず、何の区別もない座席のときにのみ円順列が使えます。
座席に番号があったり、だれかの専用座席(親とか先生など)があったら円順列は使えません。
本当は図で解説したほうが分かりやすいとは思うのですがコメント投稿欄には図が書けないのでこれが限界です。
さらにわからない時は遠慮なくおっしゃってください。
ありがとうございます。
区別したりしなかったり、ややこしいですが、今回の問題のように、番号がある場合は、区別できるから円順列が使えないんですね。
あと、もう一つですが、
(5)のサシスの求め方を上の(2)の考え方と同じようにすると、①は5通り、②は4通り、③は4通り、④は3通りで、5・4・4・3=240通りですが、これだと答えの260通りにはなりません。(2)と同じ考え方だとなぜ間違いになるのかわかりません。
なぜ、私のように考えると、20通り足りなくなっちゃうんでしょうか?
同様にセソタチも5・4・4・4・3とすると間違いですよね。(2)は5・4・3で良いのに、この考え方で、サシス、セソタチをするとダメなのが謎です。おそらく積の法則が使えないんでしょうが・・・
>本当は図で解説したほうが分かりやすいとは思うのですがコメント投稿欄には図が書けないのでこれが限界です。
可能であれば、円順列が使える条件など、記事でとりあげていただけるとうれしいです。
今回もすごくいい質問だと思います。
結論から先に伝えますと、積の法則が使えないのではなく、塗る球が3個と4個の違いで考え方が変わるからです。
3個だと球の色がすべて異ならないと隣り合う色が同じでない塗り方ができないのに対し、4個だと例えば2番と4番に同じ色を使っても隣り合う球の色を異ならせることができるのです。
例:-1青-2赤-3黄-4赤ー ←これの「-」を紐だと思って輪っかを作ってください。隣り合う色は同じになりませんよね。
同様に球が5個の時も同じ色を使えるのでこれも(2)とは違った考え方が必要です。
>可能であれば、円順列が使える条件など、記事でとりあげていただけるとうれしいです。
ありがとございます。今は国立大の入試問題の解説作成で手が回っていませんが、今後はいろいろな高校数学の問題の解説も作っていきたいと思います。
すぐにはお答えできないかもしれませんが、これからもご要望やコメントを頂けると幸いです。
>4個だと例えば2番と4番に同じ色を使っても隣り合う球の色を異ならせることができるのです。
②と④に同じ色を使えるのはわかりますが、-1青-2赤-3黄-4赤-のパターンは、5・4・4・3の240通りの中に含まれてませんか?
①は5色を使えて、5色のうち青を使い、②は青以外の4色のうち、赤を使い、③は赤以外の4色のうち、黄を使い、④は青と黄以外の3色のうち赤を使えば、-1青-2赤-3黄-4赤-になりますよね。
5・4・4・3=240通りですが、20通り足りないので、その20通りは、どんなパターンが考えられるんでしょうか?
これもごもっともな質問です。
例えば1と3に同色が入ると4は残り4色から塗る色を選べます。
例:-1青-2赤-3青-4〇- ←〇には青以外なんでもOK
この場合5・4・1・4と数えます。ですので
>②と④に同じ色を使えるのはわかりますが、-1青-2赤-3黄-4赤-のパターンは、5・4・4・3の240通りの中に含まれてませんか?
だと最後の3が同色のパターンだと4になるので、やはりこれには含めず場合を分けて考える必要があります。
確率の問題ではこのように数え方をミスすることによって答えと合わないことが多数あります。
本当にいい質問だと思います。こちらの説明の意図がうまく伝わらず申し訳ございません。
今後もご遠慮なく質問してください。
うーん、難しい(´;ω;`)
少なくとも5・4・4・3という考え方は間違いということはわかりました。
例えば、①青②赤③青④黄という塗り方だと、
④が青以外の4色使えるから、①と③の色の組み合わせによって、④が3通りになったり、4通りになったりしますね。なので、5・4・4・3の最後を3とするのはダメですね。
5・4・4・3=240通りですが、残りの足りない20通りはどのような塗り方なんでしょうか?
240通りに含まれていない塗り方の一例とかわかりますか?
確かにこの問題は誘導がないと難しいですね。
そもそも
>5・4・4・3=240通りですが、
の部分ですでに2色同色になる場合も含めて数えてしまっています。
ですので
>残りの足りない20通りはどのような塗り方なんでしょうか?
は、残りの20通りというところが実は間違いです。
ですのでもしこのように数える場合には
①同じ色を使わないで4つの球を塗る場合
②2つが同じ色で塗る場合
③2つずつ2色で塗る場合
をそれぞれに分けて数え上げなければ答えが合いません。
①は5色から4色選んで並べる5P4=5・4・3・2=120通り
②は5色から3色選ぶ5C3、選んだ3色のうち2回使う色を選ぶ3C2、同じ色を1,3に塗るか2,4に塗るかで2通り、残った2か所に2色を塗るで2P2
よって5C3・3C2・2・2P2=120通り
③は5色から2色選ぶ5C2、その2色を2回ずつ使い1,3に塗るのと2,4に塗る場所が2通りある。例えば青赤青赤と赤青赤青の2通り
よって5C2・2=20通り
これらから120+120+20=260通りとなります。
③の20通りはもちろん残りの20通りではありません。
この回答でいかがでしょうか。
お役に立てれば幸いです。
解説ありがとうございました。
>5・4・4・3=240通りですが、の部分ですでに2色同色になる場合も含めて数えてしまっています。>ですので残りの足りない20通りはどのような塗り方なんでしょうか?は、残りの20通りというところが実は間違いです。
5・4・4・3=240だから、残りの20通りの1例が20通り書けるのかと思っていましたが、書けないんですね。
私もいくら考えても、一例が見つからなかったので、無理という結論にします。不思議だなあ・・。長い間、教えていただきありがとうございました。
こちらこそ良い質問をいただいて勉強になりました。ありがとうございました。
動画や対面ではなく文章で伝えることの難しさも知ることができました。
また疑問点等ありましたら遠慮なくご質問ください。