参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022九州大大問2(文系)
問題

これは空間ベクトルの問題。
特にひねった内容はなく、教科書レベルをしっかり理解できていれば完答できる。
(1)から順番に誘導になっているので計算ミスには気を付けたい。
解説
(1) の解説
空間ベクトルには、直線の方程式や平面の方程式など教科書の例題では扱わない公式があります。
これらの公式は受験では必ず必要となりますので、この問題をきっかけにしっかりとマスターしてほしい。
解法1
最初の解法は教科書通りのやり方を紹介します。
ベクトルの垂直条件である内積が0と単位ベクトル(大きさが1のベクトル)がヒントとしてあるので求めるベクトルを文字でおいて連立します。

解法2
こちらの解法ではベクトルの外積を使います。
平面に対して垂直なベクトル(これを法線ベクトルという)を求める問題のときにこの外積が活用できます。
まずは外積の公式から
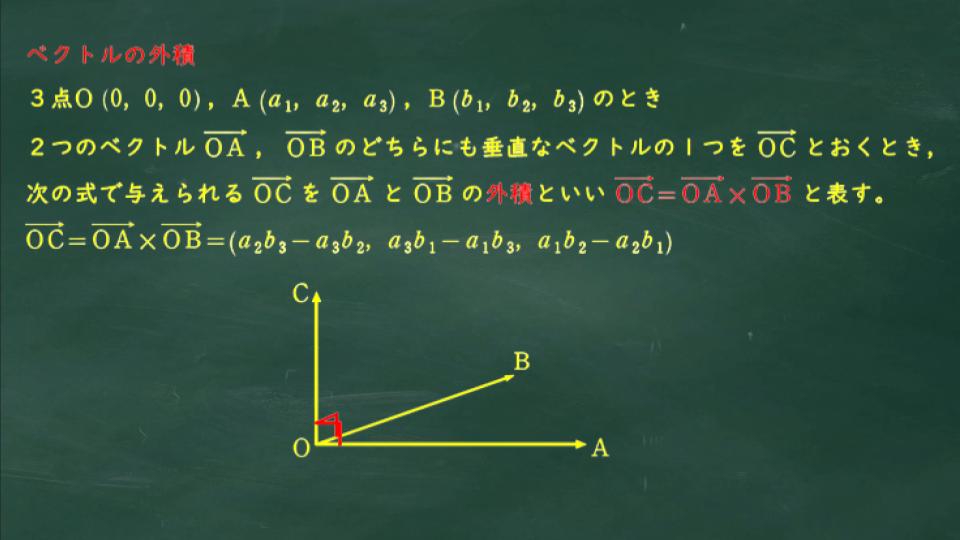
この外積の公式を用いたらあとは大きさが1であるベクトルを求めればよい。
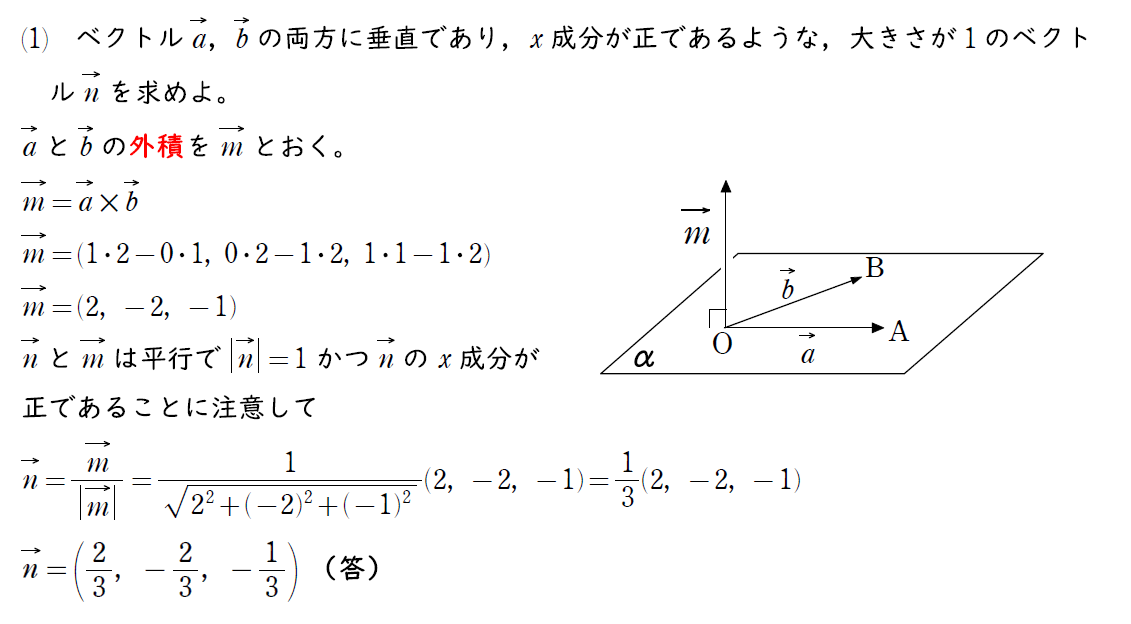
(2) の解説
点から平面までの距離を求める問題。
この問題も教科書通りのやり方と公式を用いたものの2通りの解き方があるので紹介します。
解法1
まずは教科書通りの解き方から。
垂線の足である点Qが平面 α 上にあるので同一平面上にあるための条件式を用いる。
あとは (1) で求めた法線ベクトルと平行であることを利用すればよい。

解法2
ここで用いる点と平面の距離の公式も教科書ではあまり扱われない。
この公式を用いるに、まずは平面のベクトル方程式を求める必要がある。
平面のベクトル方程式の公式は以下の通り。

次に点と平面の距離の公式をチェック
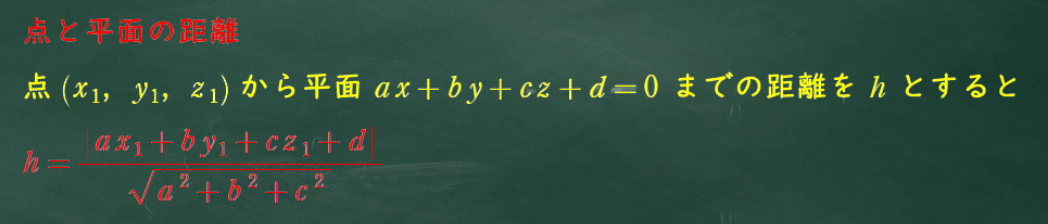
まさしくこの問題で使える公式なのでしっかりマスターしてほしい。

(3) の解説
最後の問題はあまりひねりがないので (1),(2) が出来ていれば完答できる。
問題は図を書いて把握しよう。

終わりに
教科書で扱う空間ベクトルだけでは不十分。
参考書等を利用して、今回のいくつかの公式をしっかり押さえておきたい。
ベクトルの攻略は受験生として真っ先に取り組んでほしい分野なので、いろいろな問題に触れておこう。








コメント