【2023】大阪公立大学入試問題数学大問２(理系）をとことんわかりやすく動画を使わずに解説します

参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか？

YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。

この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。

2023大阪公立大大問２（理系）

問題

数学Ⅲの複素数平面の問題。

対称な点や回転移動など基本的な問題が出題されているので、複素数平面の問題になれるにはちょうどいい難易度の問題だ。

解説

(1) の解説

これは複素数平面の問題でよく使われる方法だが、実数ｘ、ｙを用いて実数平面で説明するとよい。

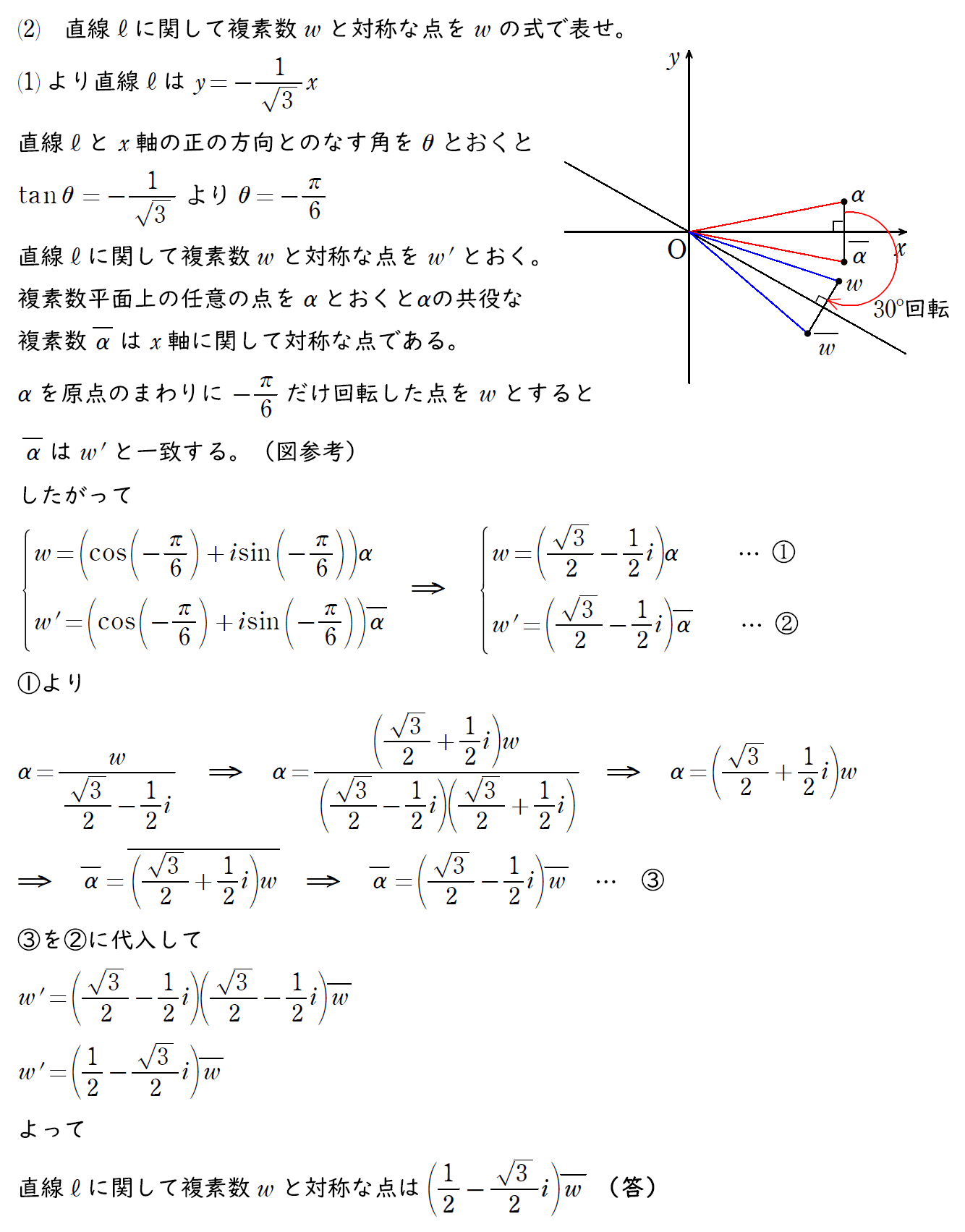
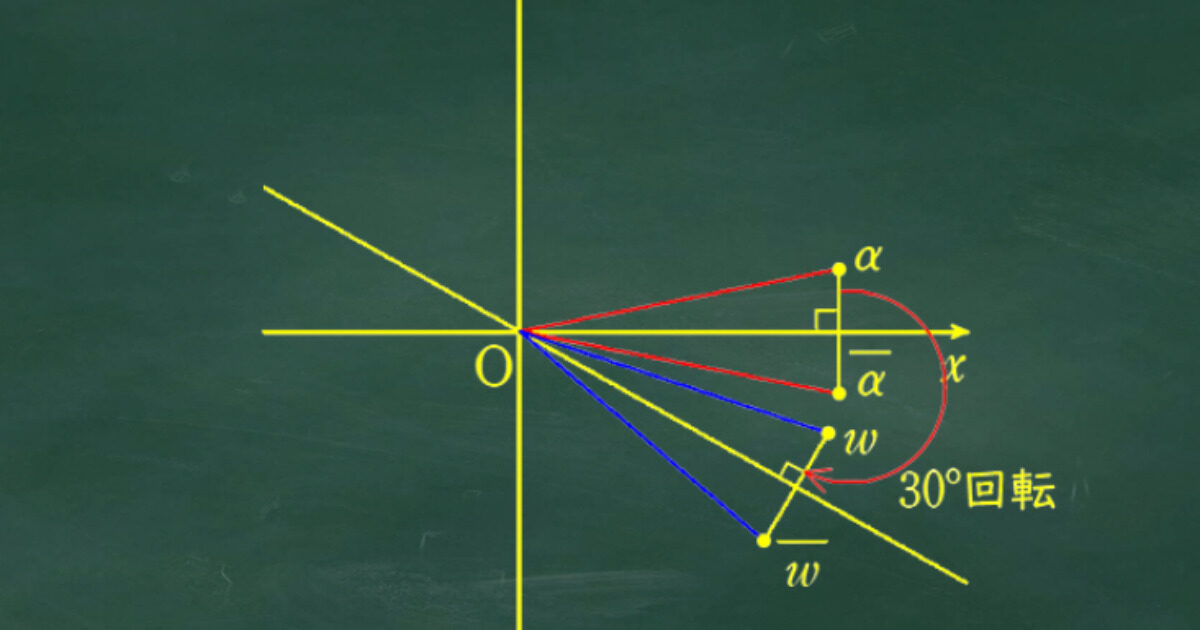
(2) の解説

これも実数平面で直線に関しての対象点を考えてもいいのだが、(1) を誘導に使って、共役な複素数の図形的な意味（ｘ軸に関して対称）を用いて考えるとよりわかりやすい。

(3) の解説

この問題は複素数平面の分野で頻出の図形(点)の回転移動の問題。

回転移動は昔、行列の分野でもよく取り上げられていたが、今はこの複素数平面で考えることになっている。

問題の上から順番に移動していき、最後は (2) の誘導を使って直線に関しての対称移動を行う。

(4) の解説

(3) で f(z) を間違えずに求めることが出来ていれば、ここも完答することができる。

(1) と同じ方法で図形の方程式を求めるとよい。

終わりに

受験生にとって複素数平面は敬遠されることが多いが、この大学の問題のように教科書をしっかり理解できていれば完答できるような難易度の問題も多い。

苦手分野と決めつけず、各大学の過去問を利用して複素数の問題になれておけば意外と得点源にすることもできる。