【2023】神戸大学入試問題数学大問２(理系）をとことんわかりやすく動画を使わずに解説します

参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか？

YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。

この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。

2023神戸大大問２（理系）

問題

数学Ⅰの２次関数と数学Ⅱの領域の問題。

図示する必要がある問題は、説明文を添えてしっかりとした図を書こう。

この問題は文系の大問１と類似しているのでそちらも参考にしてほしい。

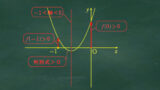
【2023】神戸大学入試問題数学大問１(文系）をとことんわかりやすく動画を使わずに解説します

参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか？YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。

toridenblog.com

2023.05.06

解説

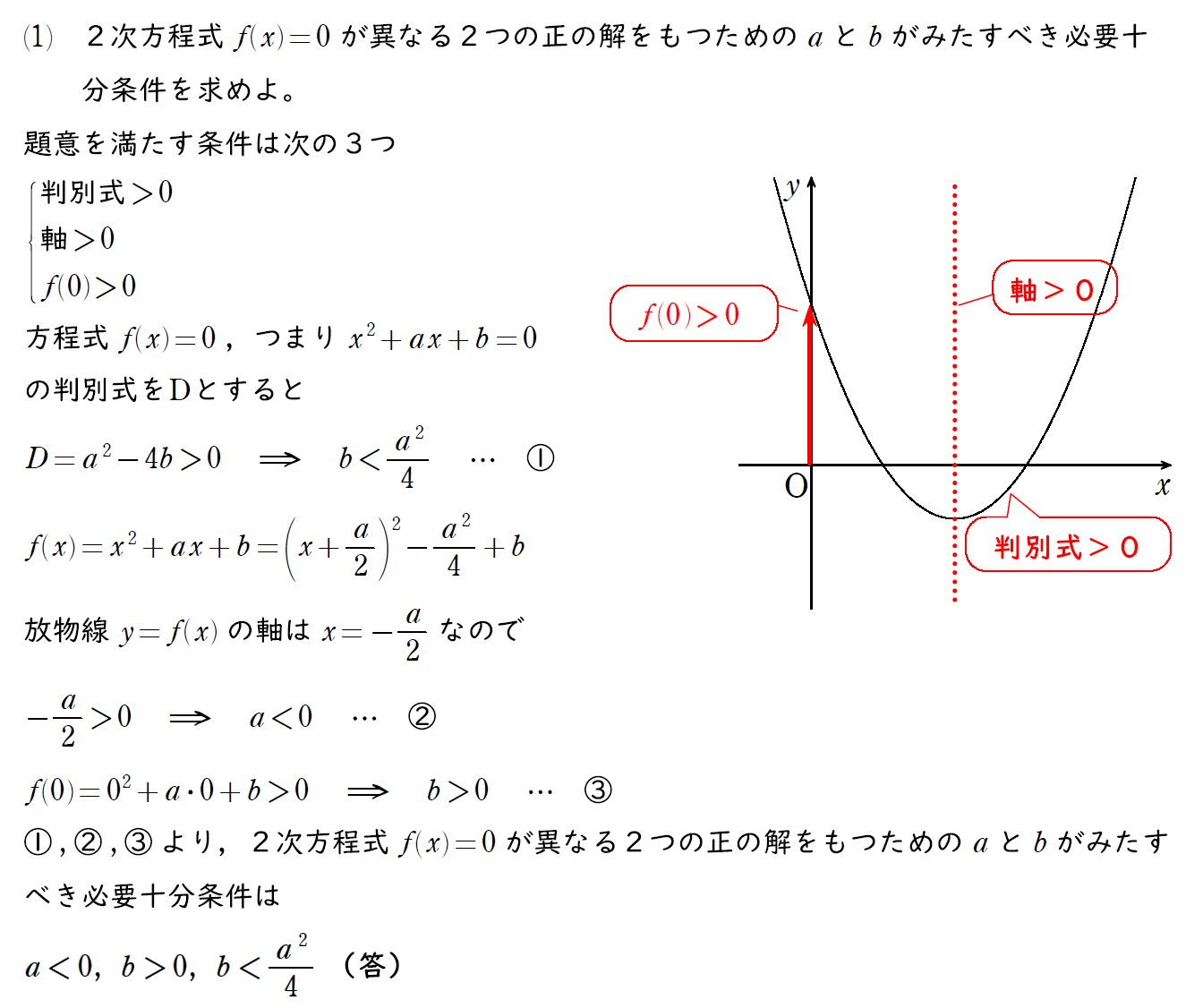
(1) の解説

実数解をもつかどうかは判別式だけでよいが、解の存在範囲が指定されているときは判別式のほかにも軸の位置や定義域の端点の符号を調べる必要がある。

(1) の別解

この別解の解答は数学Ⅱの解と係数の関係を用いて考える。

上記の解答よりシンプルに求めることができるが、あまり応用の幅が利かないのでお勧めはできない。

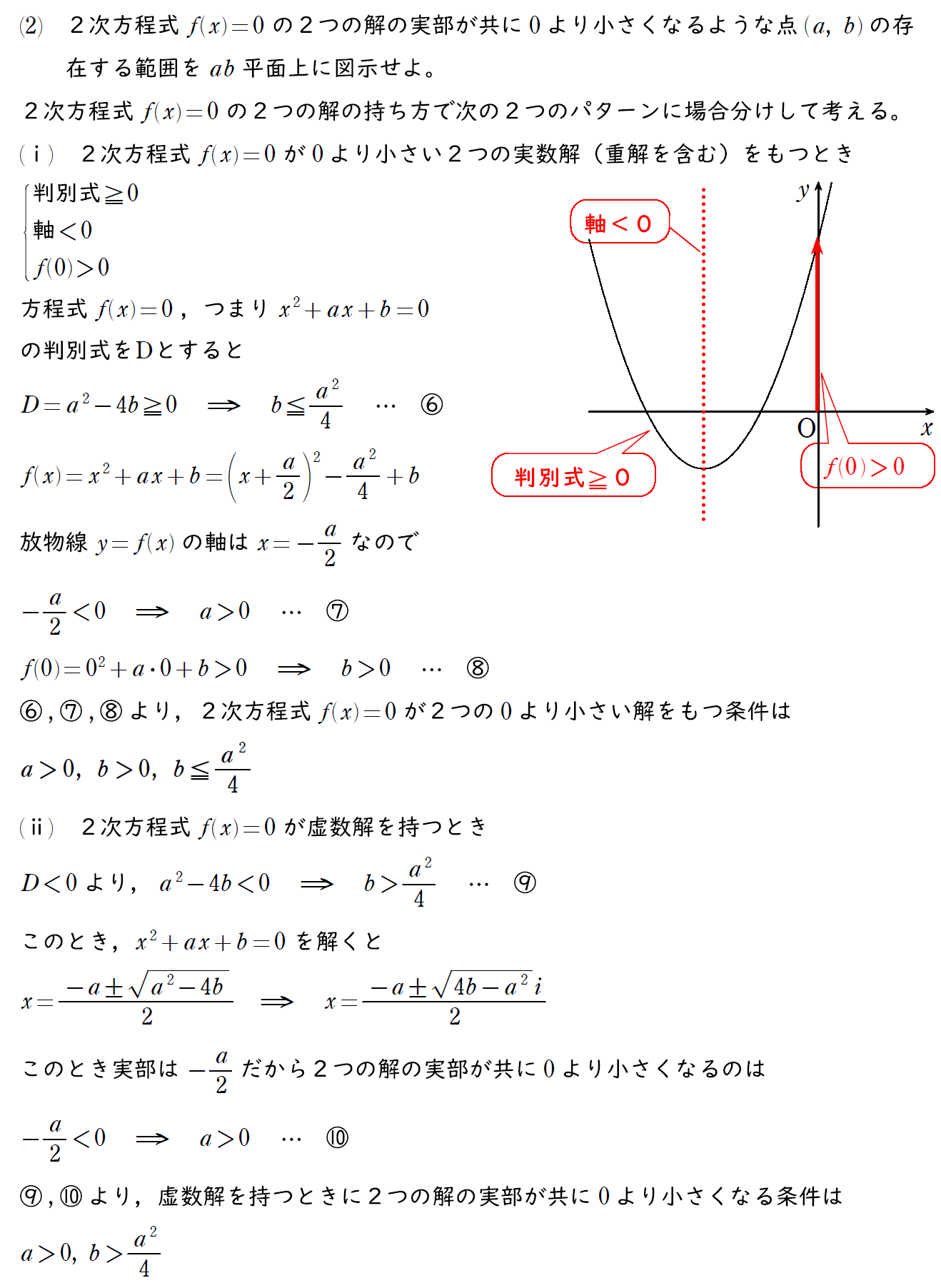
(2) の解説

問題の題意から２次方程式の２つの解が実数解に限定されていないので場合分けが必要。

実数解のときは (1) と同様に、判別式、軸の位置、端点の符号を考える。

虚数解をもつときは解の公式より、２つの虚数解を求め、実部の符号を考える。

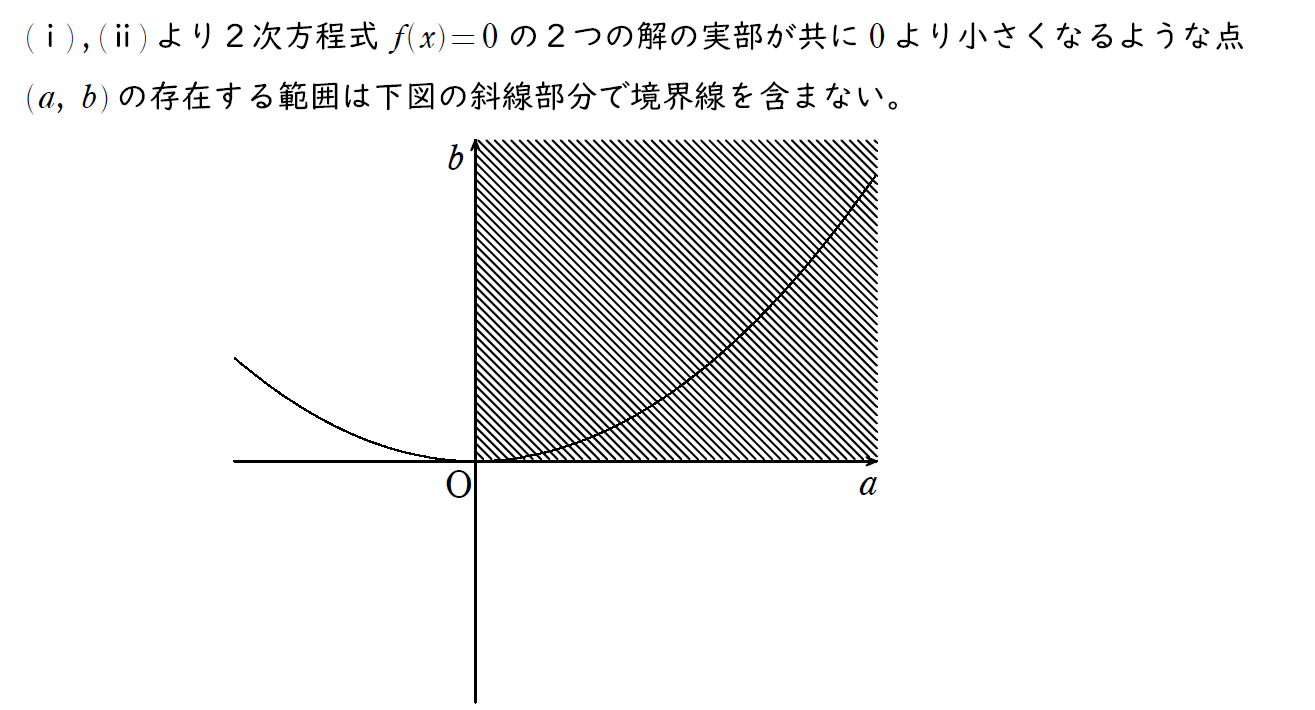
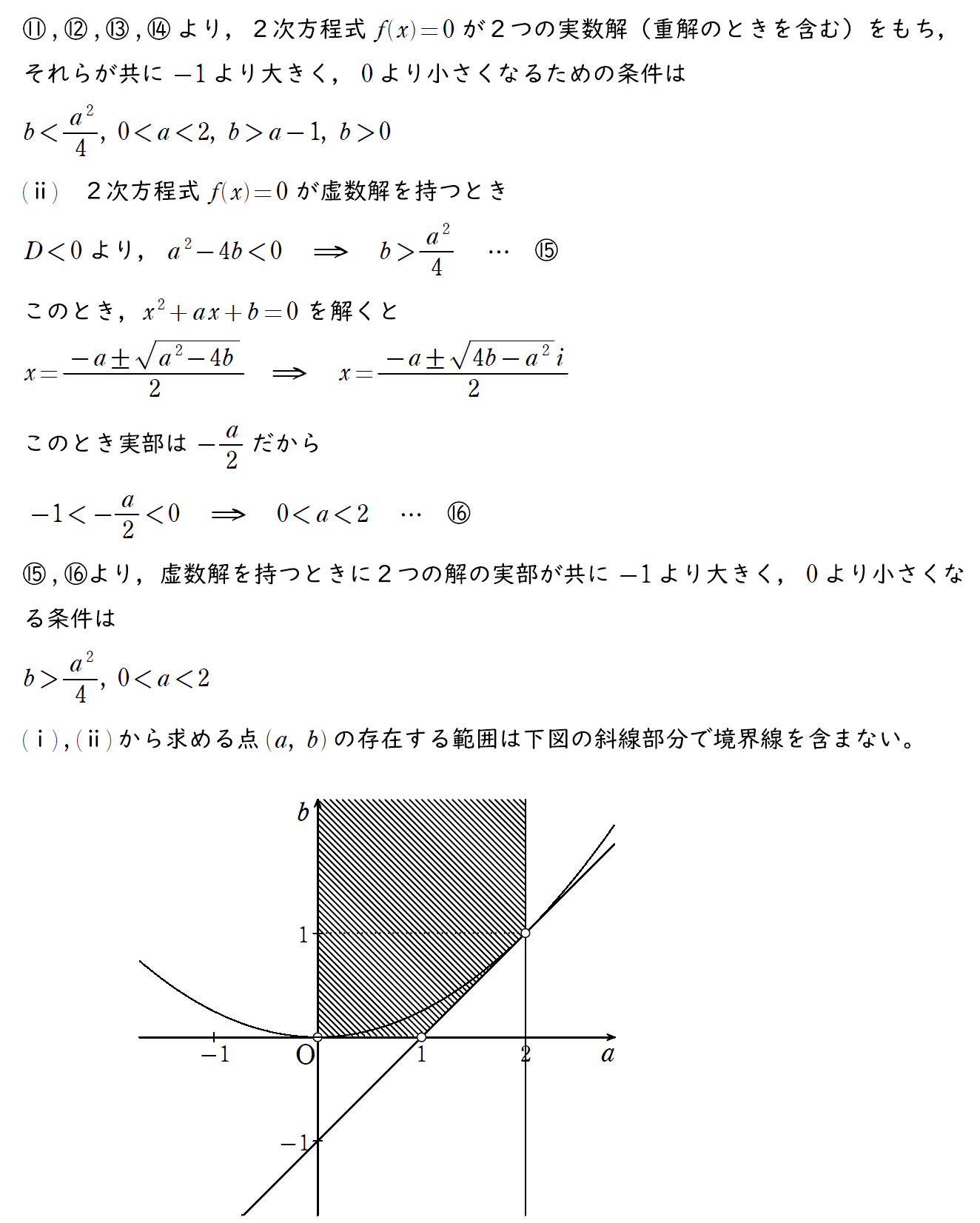
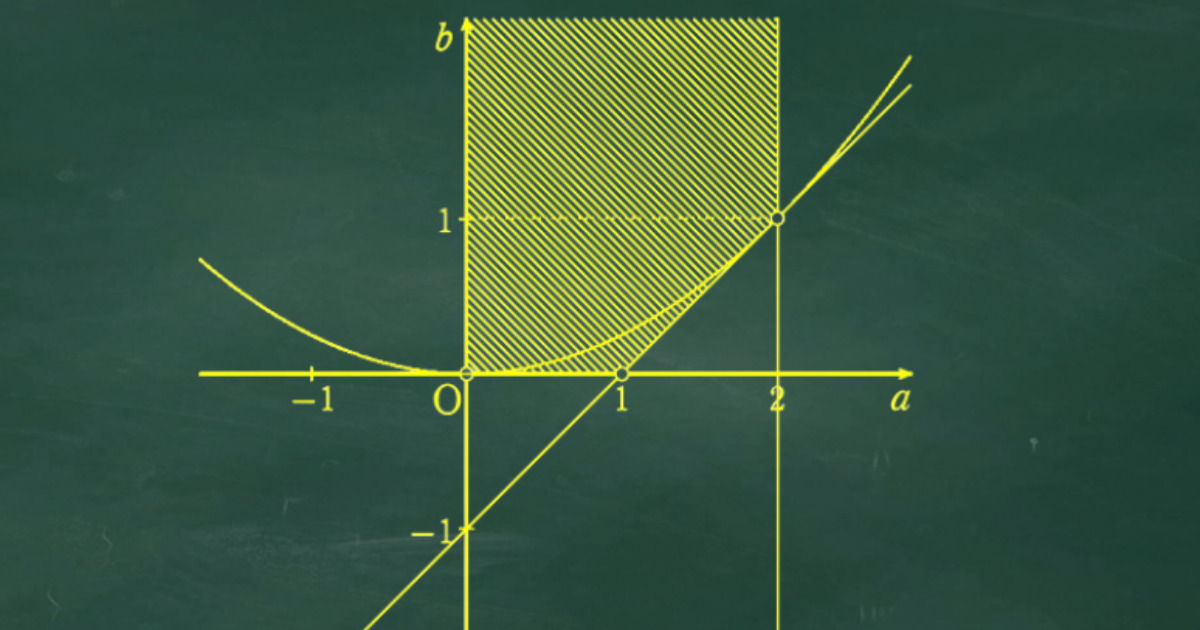
以下のように求める領域の説明を行ってから、図をしっかり書こう。

特に境界線の説明は大切だ。

(3) の解説

これも (2) と同様に実数解をもつときと虚数解をもつときの両方を考える。

難易度は (2) からは上がっていないので丁寧な解答を心がけ、完答を目指そう。

終わりに

この問題は文系の大問１番と類似している。

難易度的には文系も理系もさほど変わらない。

教科書で扱うレベルの問題なので取りこぼさないように注意して完答を目指してほしい。