【2024】大阪公立大学入試問題数学理系大問２をとことんわかりやすく動画を使わずに解説します

参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか？

YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。

この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。

2024大阪公立大大問２（理）

問題

数学Ⅱの複２次式と数学Cの複素数平面の問題。

前半は解の存在を判別式を用いて考える。

後半は複素数平面上の話だが、そこまで複雑な複素数の知識を使うわけではない。

解説

問１の解説

複２次式の問題。

まずは文字を置き換えて２次式にして考える。

４つの虚数解を持つ条件は２通りあるので場合を行い求めていく。

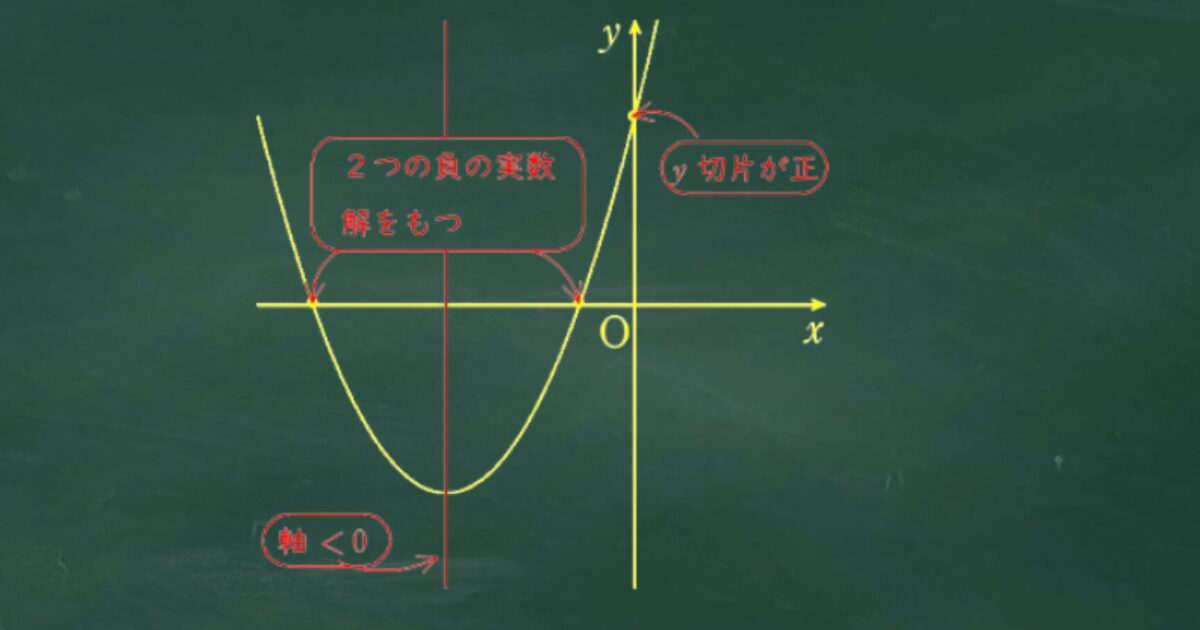
(ⅰ)は数学Ⅰの２つの負の解をもつ条件を考える問題。

問２の解説

ここでは実際に４次方程式を解いていく。

まずは問１でおき換えたｔの２次式を解くのだが、解の公式を用いた後、虚数解であることに注意が必要。

その後は２重根号を解消していく計算になる。

この解説では複合(±)を用いてないので多少解説が長くなっているが、内容自体はそこまで難易度は高くない。

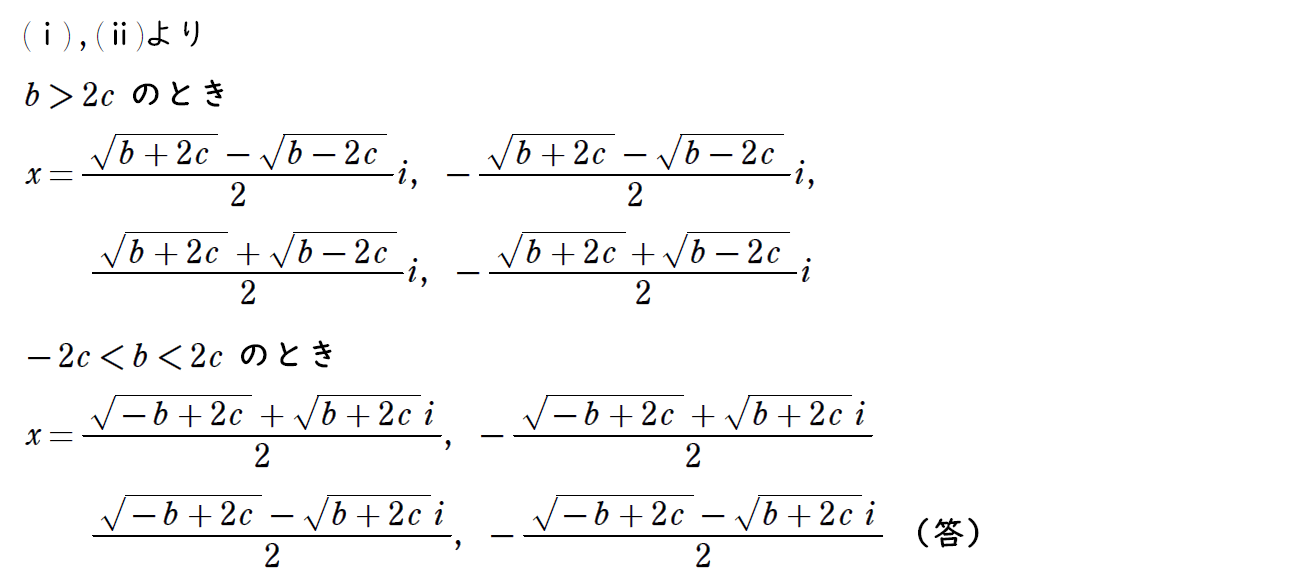
問３の解説

問２から同一円周上に４点があるときをすぐに見つけることができる。

あとは複素数の大きさを使って確かめるだけ。

問４の解説

こちらも問２から同一直線上にある条件がすぐに見つかる。

あとは等間隔に並ぶための条件を考えればよい。

終わりに

めんどうな計算部分はあったが、全体的に難易度は高くない。

複素数平面の問題と構える必要はなく、誘導にしっかり乗っていけば完答が目指せる。

計算部分は少し大変なので、しっかり練習しよう。