参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2023大阪公立大大問4(文系)
問題

2次関数の最小値問題。
2点間の距離を用いるのでルートが付くが、ルートの中身だけ取り出して2次関数として扱えば難易度は高くはない。
解説
(1) の解説
後のことを考えると、点 P も文字でおいて計算を進めたい。
ルートの中身の2次関数の最小値を考えればいいのだが、定義域があることに注意する。

(2) の解説
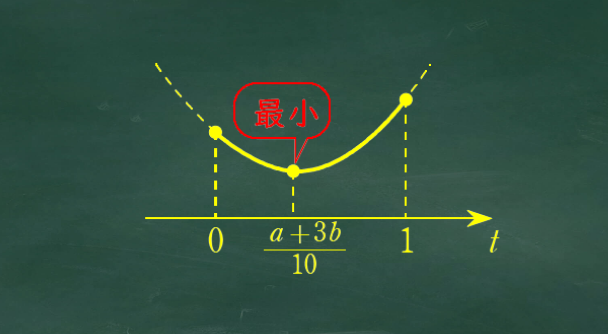
(1) で作った f(t) の2次式を平方完成して、頂点と軸を求める。
文字が入って複雑だが、この手の問題は頻出なのでしっかり練習しておこう。
軸の値と定義域の位置関係によって場合分けを行う。
これも教科書をはじめ問題集などでもよく取り上げられているので、解法をマスターしておきたいところ。

(3) の解説
(2) を利用してそれぞれの場合について求めていく。
① の場合の計算が一番大変だ。
② , ③ は高次方程式だが、工夫して解くとそんなに難しくはない。


終わりに
2次関数の最小値問題は入試の頻出分野である。
多くの受験生は練習を積んでいると思うが、この問題のように計算が複雑だと完答するのが難しい。
普段の演習時から最後の答えにたどり着くまでしっかり計算を行い、完答する練習をしておこう。









コメント