【2023】東京工業大学入試問題数学大問４をとことんわかりやすく動画を使わずに解説します

参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか？

YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。

この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。

2023東工大大問４

問題

数学Ⅲの立体図形の体積問題。

東工大では頻出の分野である。

この年の立体図形はそこまで複雑なものではないのでしっかり図を書いて完答を目指そう。

ただし、計算量は多めなので、計算力を付けて臨んでほしい。

解説

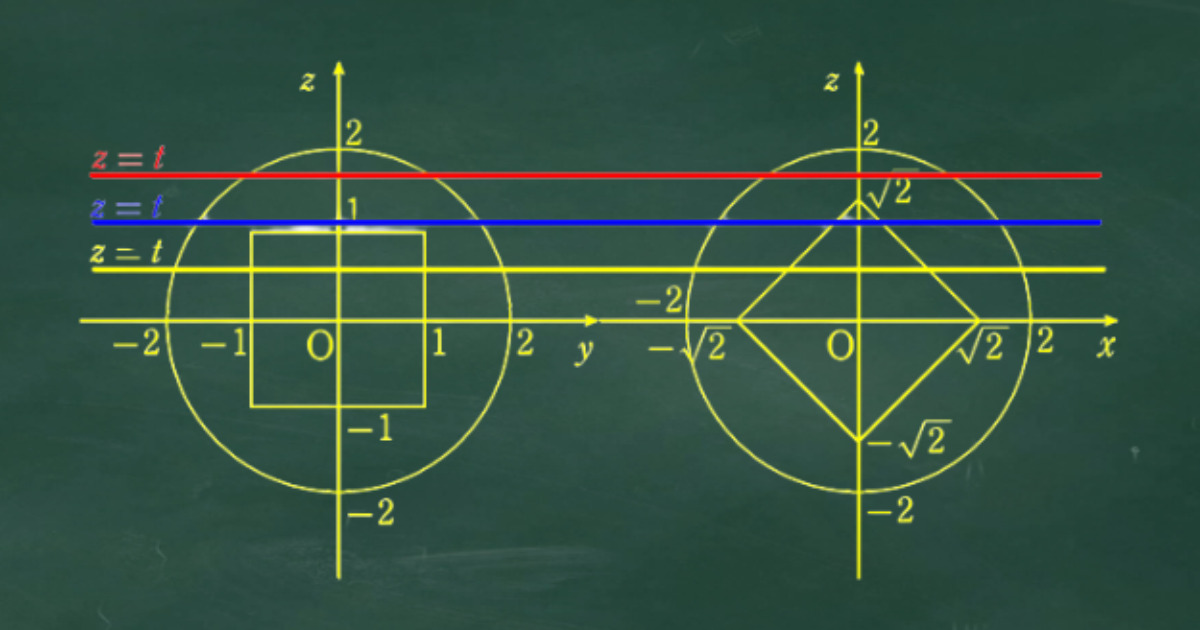
まずは図形Aと図形Bを問題文から把握し、各座標平面と交わる面を図示しておこう。

さらに空間図形では定番の座標平面と平行な任意の面で切り取った図形の面積を考える。

この問題ではいくつかの場合によって切り取る図形の形が違うので場合分けを行って処理していく。

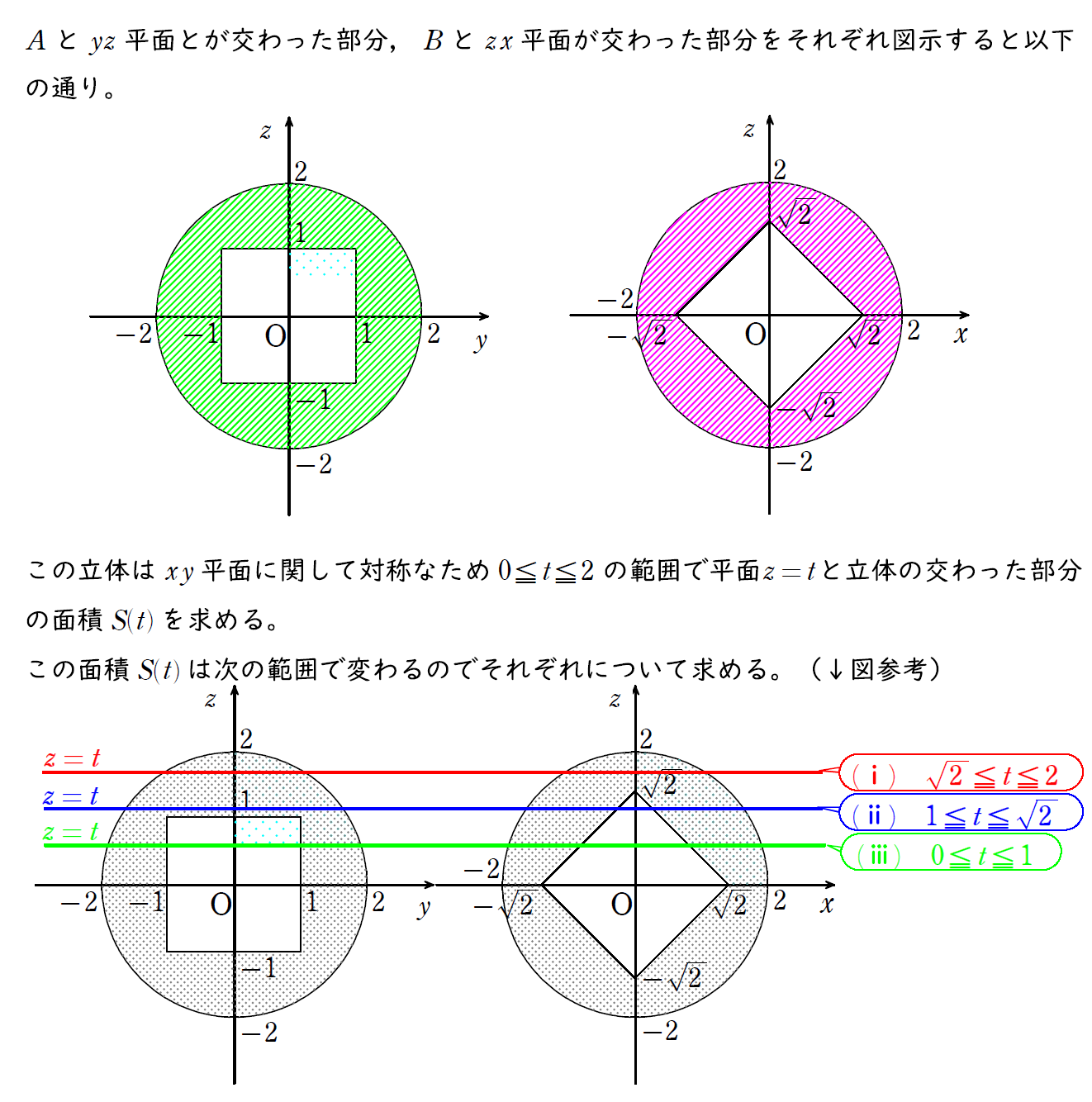
３つあるうちの１つ目の場合。

くり抜かれる部分がないので面積は下図のような正方形となる。

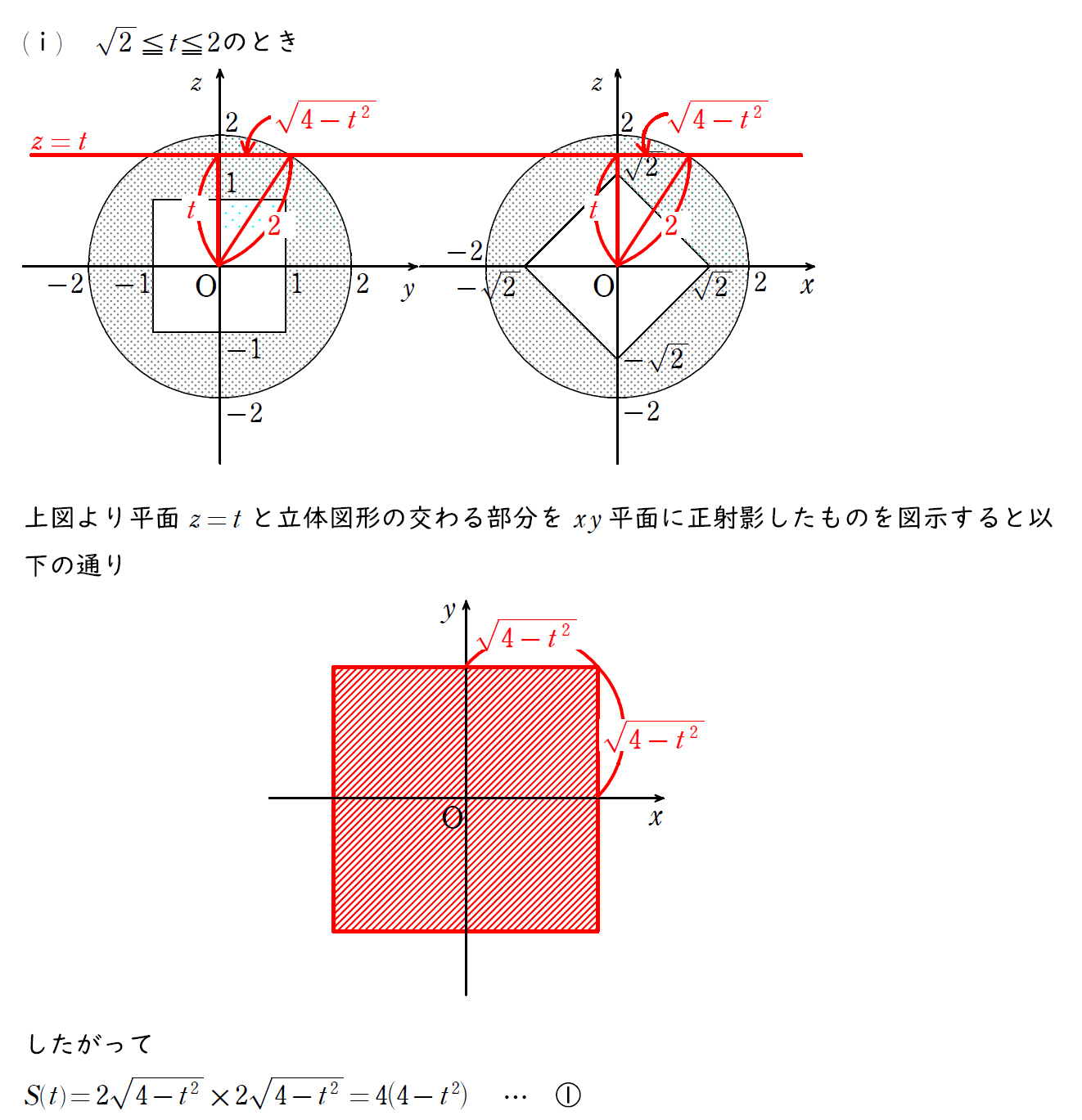
２つ目の場合の面積。

ｘｙ平面上に正射影して表すと下図のように真ん中部分がくり抜かれる。

したがって、長方形２つの面積の和となる。

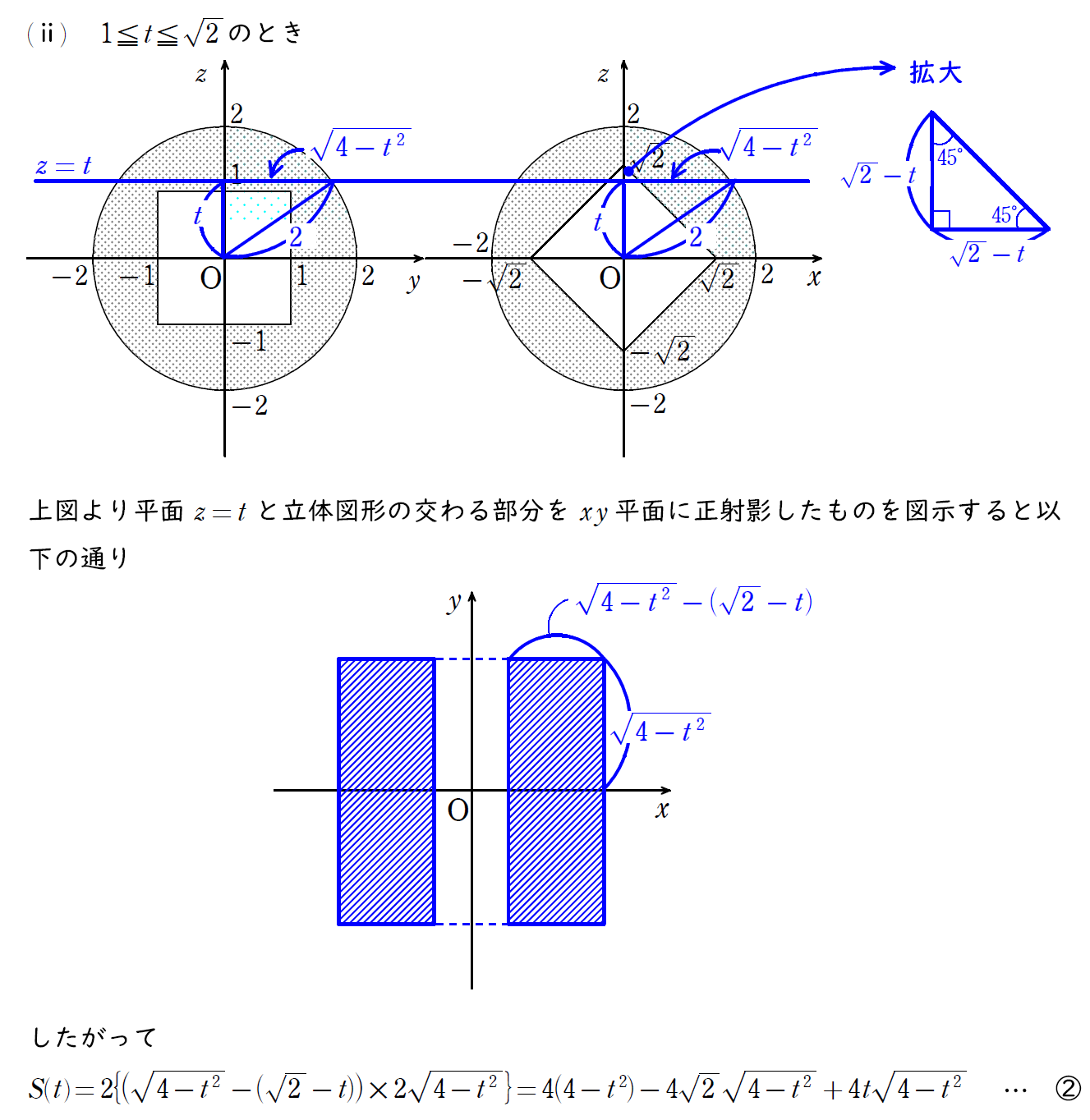
３つ目の場合の面積。

これは上下左右にくり抜かれる部分があるため、下図のように４か所の長方形の和が面積となる。

ここからは積分計算。

そこまで複雑な計算ではないが、計算量が多いので整理整頓して処理してほしい。

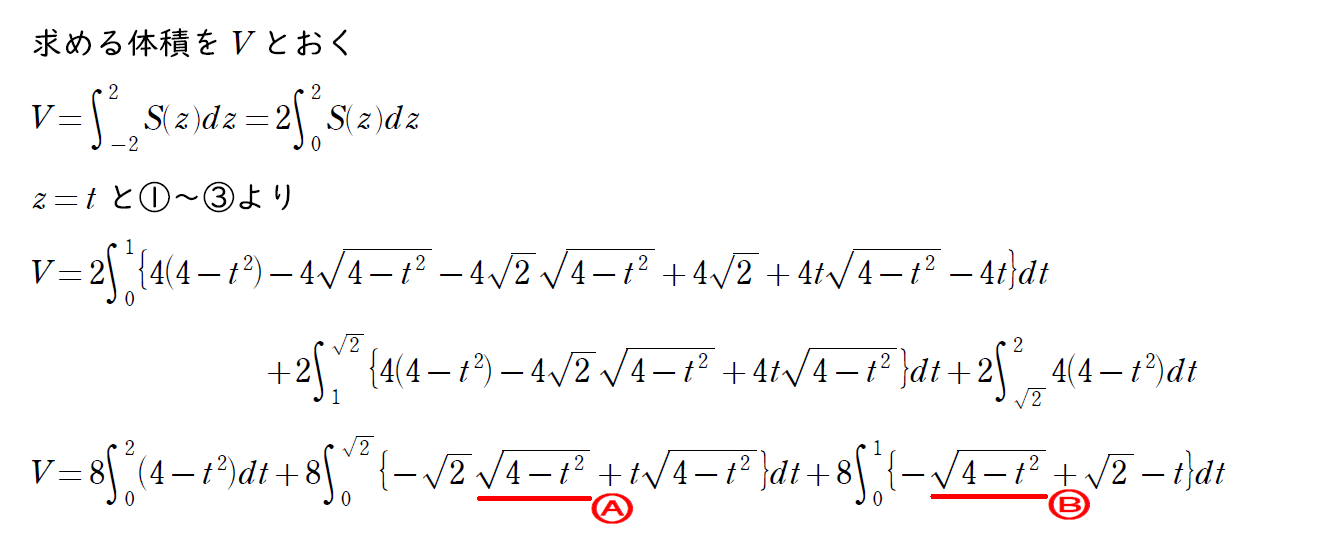
一部分置換積分を用いるので以下の解説のようにそこの部分だけ取り出して考えたほうが良い。

円の面積として考える方法もあるので工夫して解こう。

上でばらした定積分の値を含めてすべての部分を計算する。

しっかり時間をかけてケアレスミスしないように心がけよう。

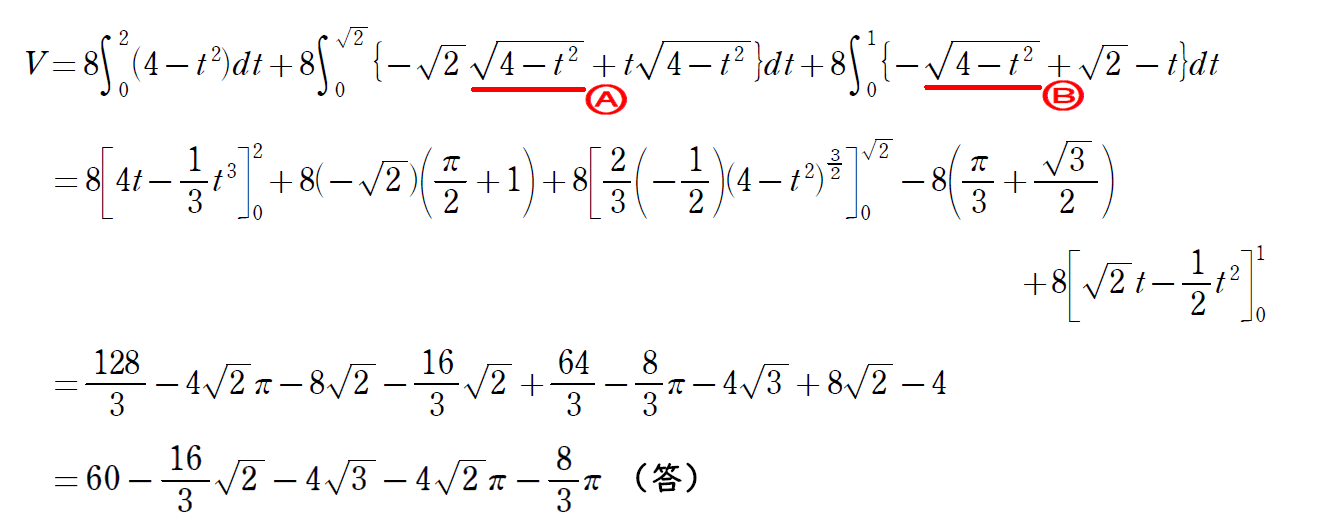
終わりに

計算には時間がかかるが東工大の体積問題としてはひねりがなくオーソドックス。

各座標平面に平行な切り口の面積を求めるのはしっかり演習を重ねておけばそれほど難しさを感じないだろう。

とにかく頻出問題は徹底的に演習しておく必要がある。