【2023】横浜国立大学入試問題数学大問１(文系）をとことんわかりやすく動画を使わずに解説します

参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか？

YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。

この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。

2023横浜国立大大問１（文系）

問題

数学Ⅱの微分積分の問題。

共通接線を求める問題と直線と曲線で囲まれる部分の面積を求める問題。

どちらも入試ではよく出題されるものなのでしっかり解法をマスターしてほしい。

解説

(1) の解説

共通接線を求める問題だが、まずはそれが１本しかないことを証明する。

接点を文字で置き、判別式を用いて求める。

文字で置いた接点の値が１つしかないことが示せれば、共通接線は１本しかないことの証明となる。

ここはあまり証明することを意識せず、接線を求めることを考えるとよい。

(2) の解説

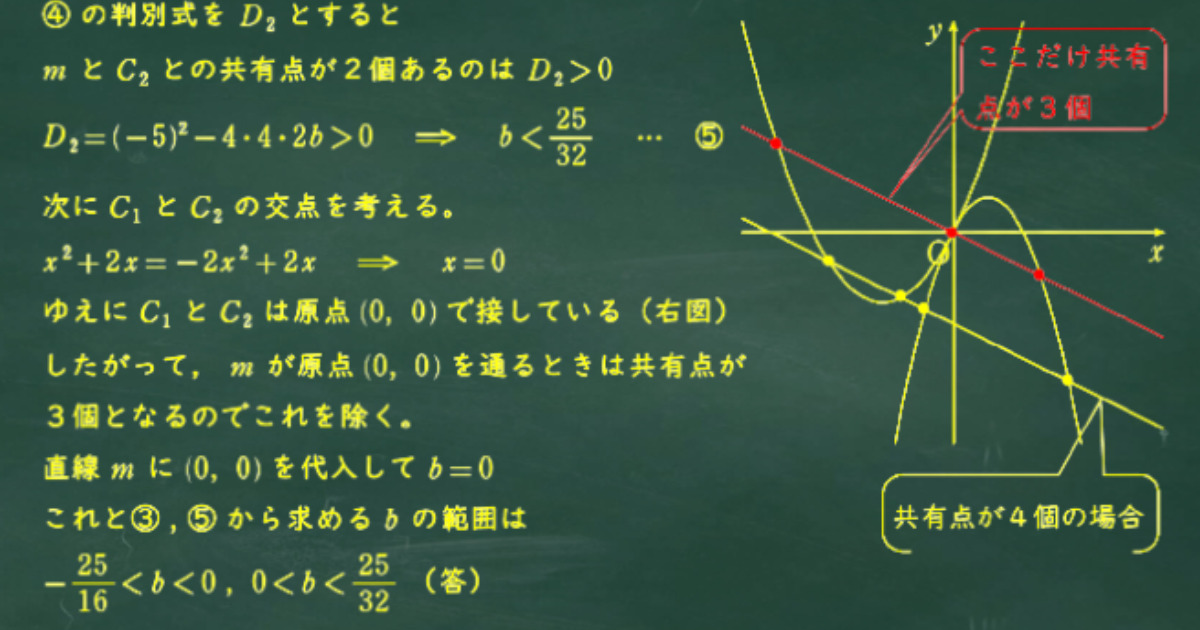
共通接線に直交する直線 ｍ がＣ_１とＣ_２とそれぞれ２交点を持つ範囲を判別式を用いて調べる。

ただし、接点を通る時だけ注意が必要。

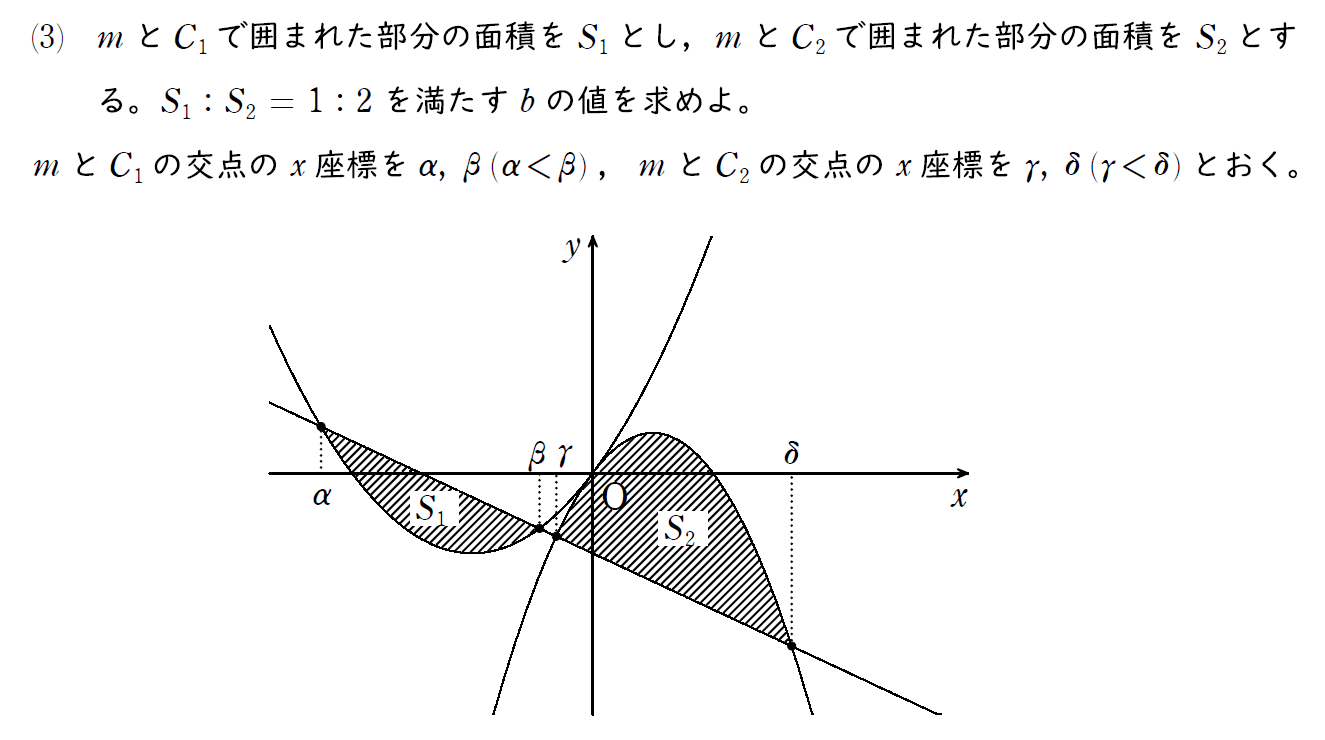
(3) の解説

(2) で求めた範囲で２つの放物線 C₁、C₂ と直線 ｍ で囲まれた部分の面積 Ｓ_１、Ｓ_２ をそれぞれ求める。

ただし、それぞれの交点を直接求めるのは大変なので、解と係数の関係を用いて解く。

その際、囲まれる面積の公式いわゆる1/6公式を用いる。

終わりに

大学入試では文系数学の範囲で微分積分の分野は頻出分野である。

特にこの問題のような、接線の問題や面積の問題は文字が入って計算が複雑になってもしっかり解ききれるように練習をしておこう。