参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすく、どの参考書よりも細かく解説をしていきます。
2022千葉大大問2
問題


この問題は面積やなす角の問題ね

数学Ⅰの知識で解けるけど数学Bのベクトルを使っても解けるよね

私は数学ⅠAまでしかわからないから数学Ⅰまでの範囲で説明してね

本当は数学Bで解く方が簡単なのにな。こっそり別解を作っちゃおう
小学校で三角形の面積は

と習ったけど高校では次の2つの公式があるよ
数学Ⅰの三角比で習う公式
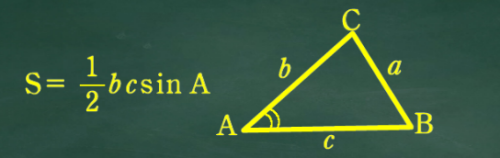
数学Bのベクトルで習う公式
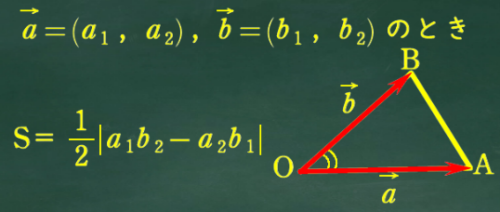
(1) は中学入試でよく出てくる次の考え方を使って求めてみよう

解説
(1) の解説1
図1
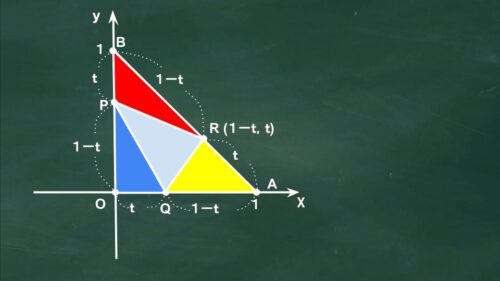

点Pと点Qの座標はすぐに求められそうね。

点Rを求める時だけ少し数Ⅱの知識を使うよ
内分点の公式



△OABと△OPQは直角三角形だから求めやすいね。△QRAと△BPRはどうやって求めるの?

点Rの座標を利用すれば求まるよ。次の図2と図3を参考にしてね
図2
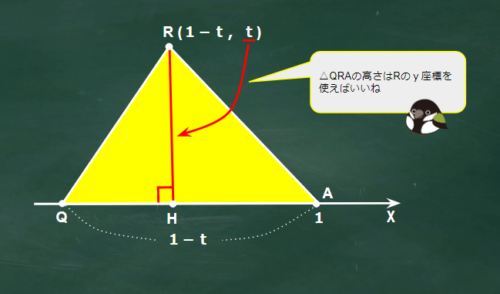

図3
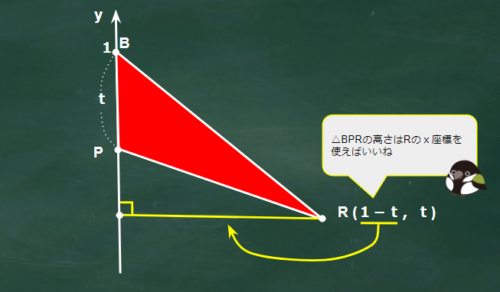

ここまでは数Ⅰの範囲で解いたけど次の解答は数学Bのベクトルの面積公式を使うよ。
(1) の解説2
3点 P,Q,R の座標を求めるところまでは一緒なのでその続きからの解説だよ

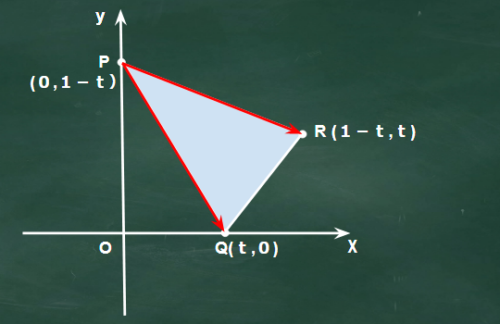

㊟の解説

やっぱり数学Bの面積公式を使った方が早いけど、最後の絶対値を外すところは注意が必要だね。
2次式の符号を調べるには平方完成をしましょう。
(2) の解説
- 二等辺三角形になるのはどの2辺が等しくなるかを考える
- tに範囲があることに注意し、合わない場合は答えから外す


結局3つともあてはまったね。tの範囲はそんなに影響なかったね

記述の解答ではたとえ答えが「適する」となってもちゃんと条件を満たしていることを解答に書かないと減点されるよ。
問題文で設定された文字には範囲があるものが多くあります。この範囲を満たしてない答えをはじくことはもちろんですが、満たしている場合でも解答に書きましょう。
(3) の解説1
(3) も数学Ⅰの三角比と数学Bのベクトルの両方で求めることができるよ。
まずは数学Ⅰの範囲で出てくる「余弦定理」を使って cosθ の値を求めてみるよ
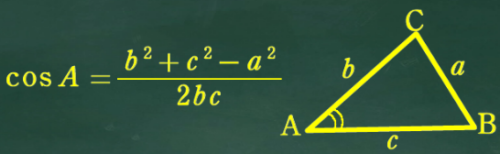

これもベクトルを使って解くやり方があるよ。
次の解説2で説明するね。
(3) の解説2
ベクトルの内積の公式で cosθ が出てくるよね。
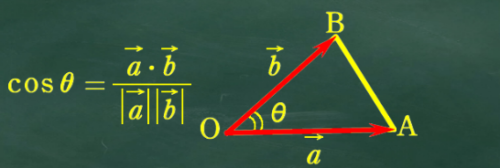

三角比の余弦定理とベクトルの内積のどちらで作っても cosθ の式は同じになるんだね。

私はベクトルはわからないから余弦定理で解いたよ

僕はベクトルの方が好きだな
入試問題ではこの問題のように (1) や (2) で求めた値を使って (3) を求める問題が多いです。前半で計算ミスをしてしまうと全滅する恐れがあるので見直しを念入りに行いましょう。
終わりに
図形の問題は小学校,中学校,高校とすべての考え方や公式を網羅してとりくむ必要があります。
一つの分野に凝り固まらずいろいろな角度から図形問題に取り組んでみよう。









コメント