参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2024令和6年度大学入学共通テスト数学2B大問4
2024年度の数学ⅡBの大問4は例年通り数列の分野から出題された。
他の大問同様、かなり誘導が丁寧になっている。
後半では数学的帰納法の証明法と命題の真偽を考えさせる問題となっている。
(1) 問題
難易度☆
等差数列の漸化式の問題。
漸化式そのものが分かりやすい上、誘導が丁寧に行われているので完答を目指したい。

(1) 解説
第2項と第3項を順に求めていく。共通テストに限らず数列を把握するうえでよく使われる方法。記述でも使えることを覚えておこう。

(2) 問題
難易度☆
これも教科書の例題レベルの漸化式。(1)みたいに丁寧な誘導はないが、これも完答を目指せる問題だ。
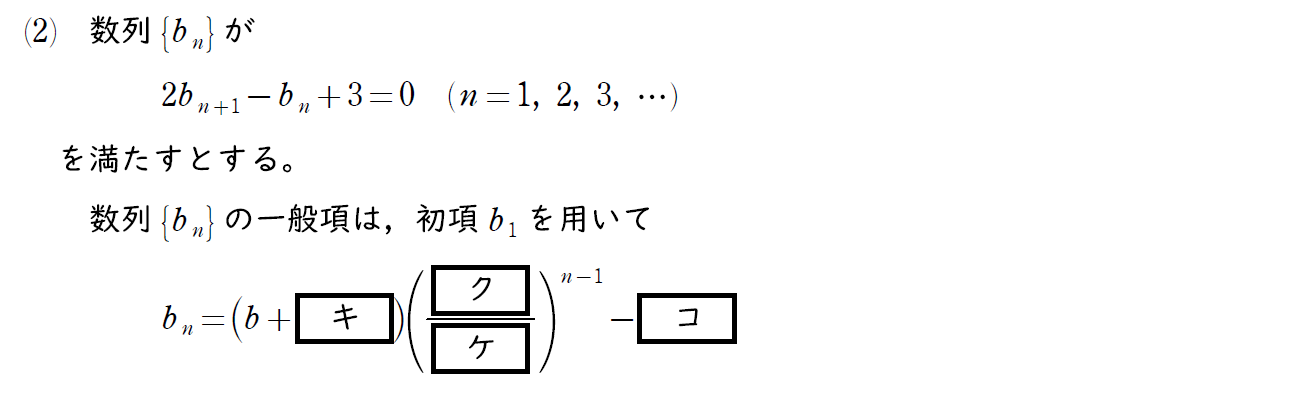
(2) 解説
特性方程式を作り、等比数列の漸化式に形を変形する。初項と公比を求めよう。

(3) 問題
難易度☆☆
前半はやはり初項から順番に求めて数列の特徴を掌握していく。
後半は数学的帰納法を問う問題で過去にも出題されたことはあるが、難易度は低め。
最後の命題の真偽もここまでの誘導された内容をしっかり把握できていれば真偽に迷うことはない。



(3) 解説
ここでもnに直接数字を代入して初項から順番に求めていこう。
命題の真偽は対偶を利用した証明方法も用いるので数学Ⅰの内容をしっかり思い出しておこう。


終わりに
この大問4の数列も今年は難易度が低めだった。取り扱う数列もシンプルだし、計算量も少ない。
来年からスタートする新課程での難易度がどう変わるかが気になるところ。
数学ⅠAに比べると全体的に取り組みやすい内容が多いので全国平均もかなり高かった模様。









コメント