参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2022横浜国立大大問2(理系)
問題

個数の処理の問題。
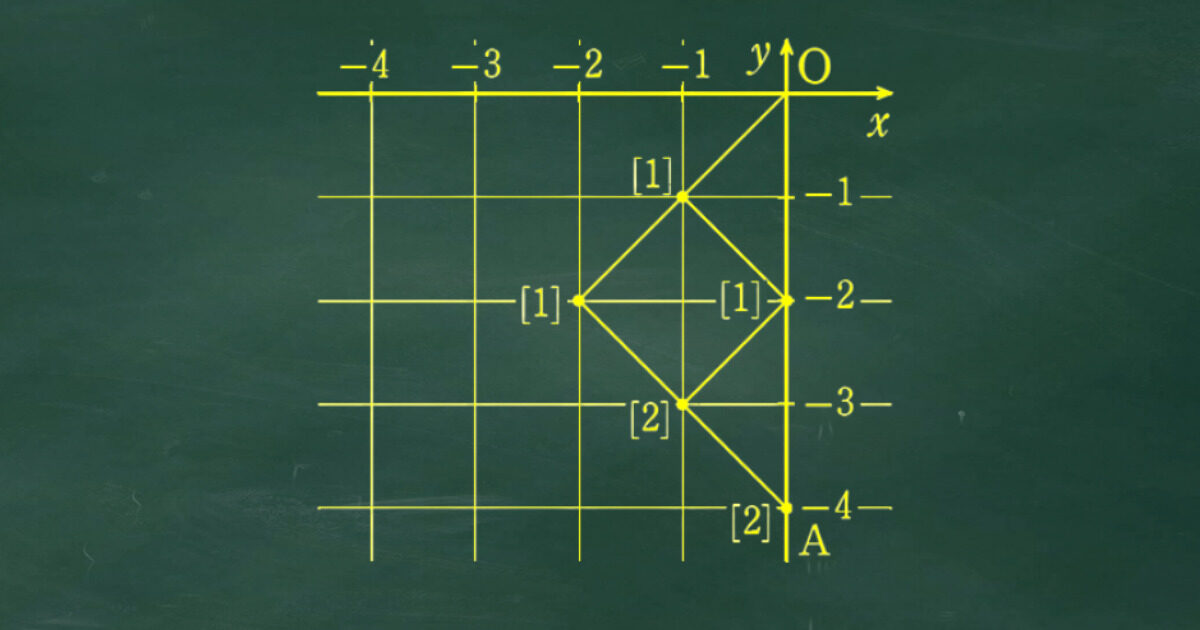
樹形図を作って場合の数を数えるのだが、以下の解説のように座標軸を使って数え上げるとミスを防げる。
公式を使うことなく数え上げるだけだが、後半は教科書にも登場する最大値・最小値の問題となっているので解法をマスターしたい問題。
解説
(1) の解説
これは以下の解説のように複雑な問題ではないので普通の樹形図を書くと簡単に求めることができる。

(1) の補足
この問題だけ考えると解答は上のように作ればいいのだが、(2) 以降の考え方のサンプルにもなる問題なので複雑なものを処理する前にここで座標軸を使った解き方を考えておくとよい。
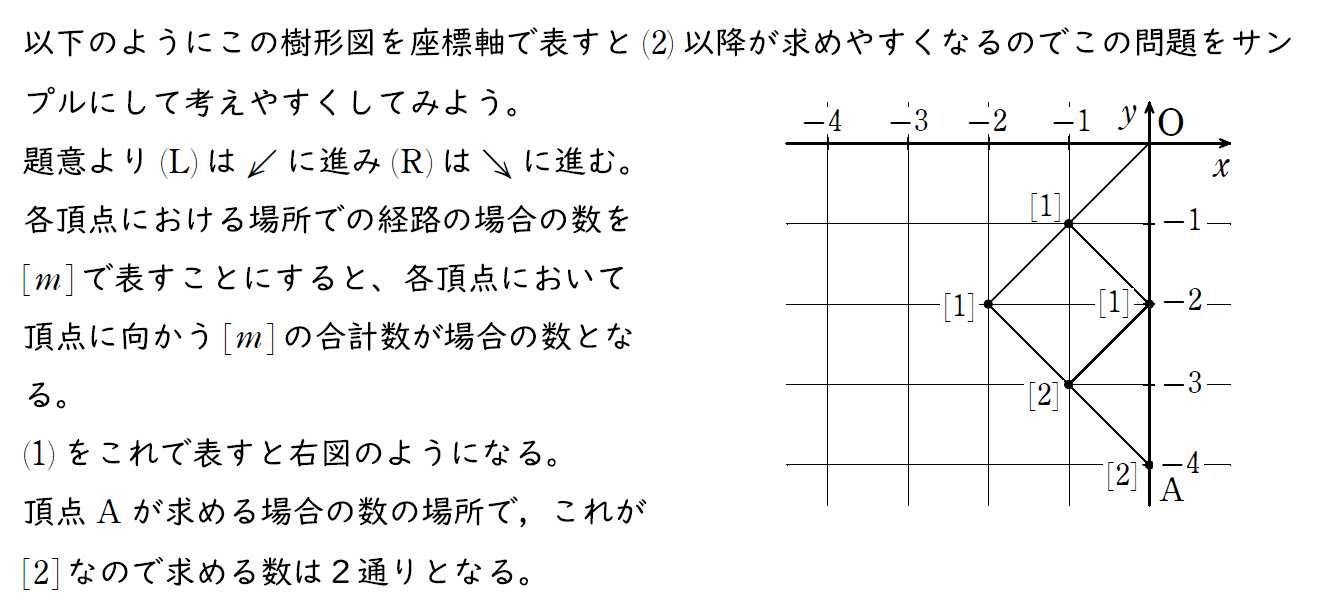
(2) の解説
(1) のサンプルをもとに考える。
(2) 以降は少し複雑になるが、丁寧に図を書くとしっかりミスなく数え上げることができる。
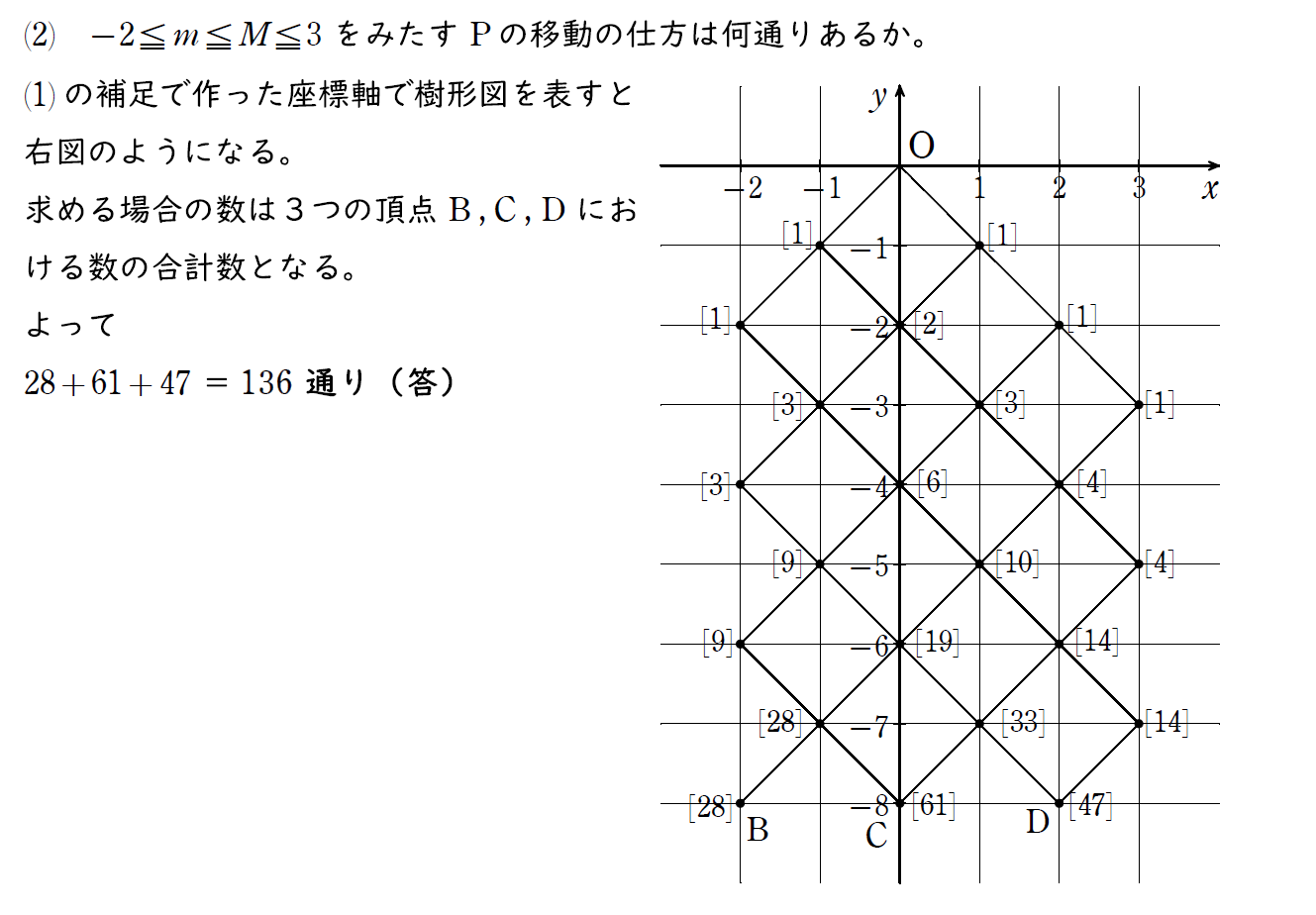
(3) の解説
最小値がー2になることを意味する問題。
教科書にも登場するがこれは「ー2以上になる場合」から「ー1以上になる場合」を取り除けばよい。
場合の数でよく見かける問題なのでしっかりマスターしよう。
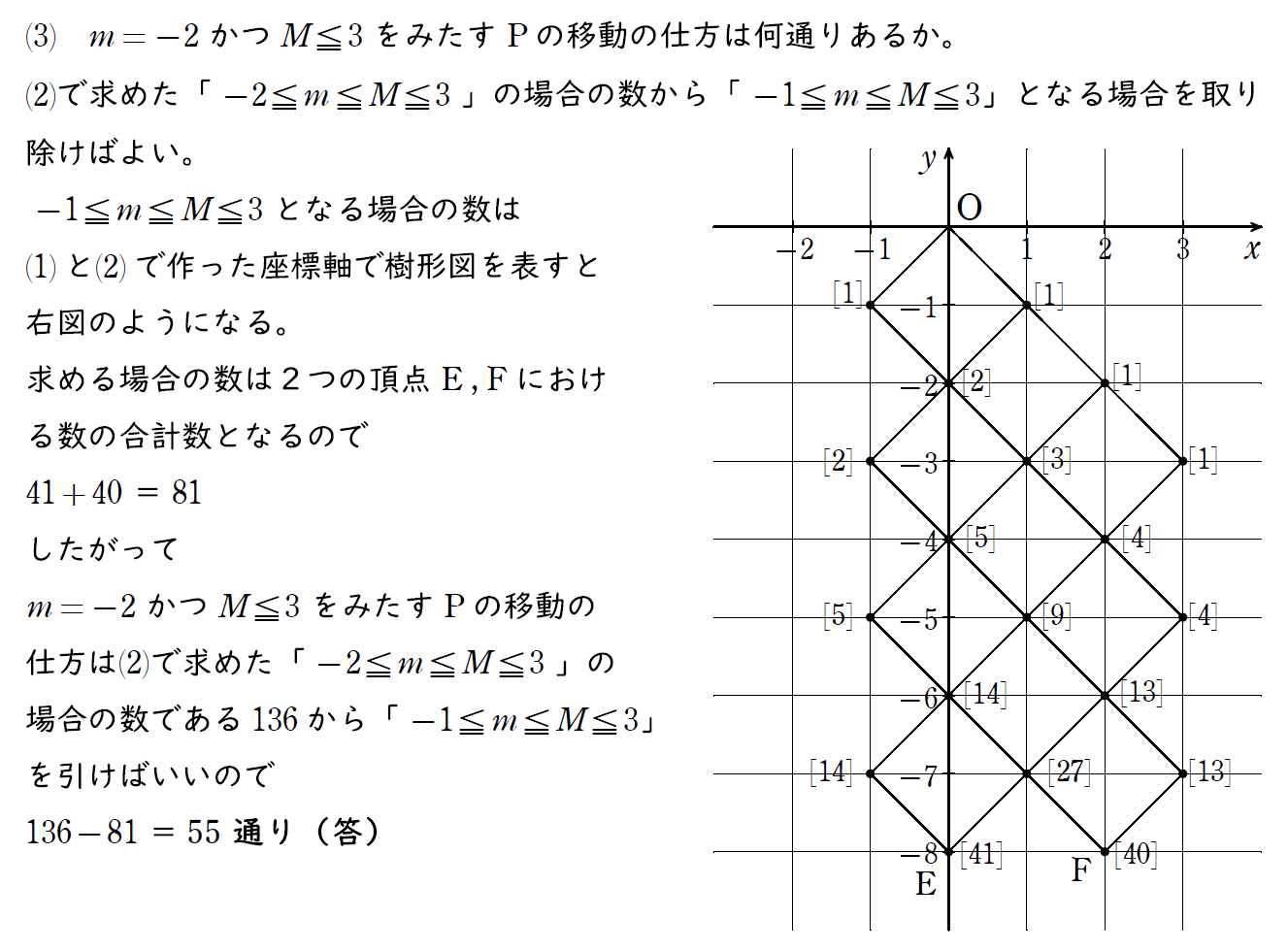
(4) の解説
(3) をもう少し複雑にした問題だが、考え方は同じ。
最大値、最小値とも取り除くという考え方を使う。
これは「少なくとも~」という場合の数頻出の余事象の考え方を用いている。
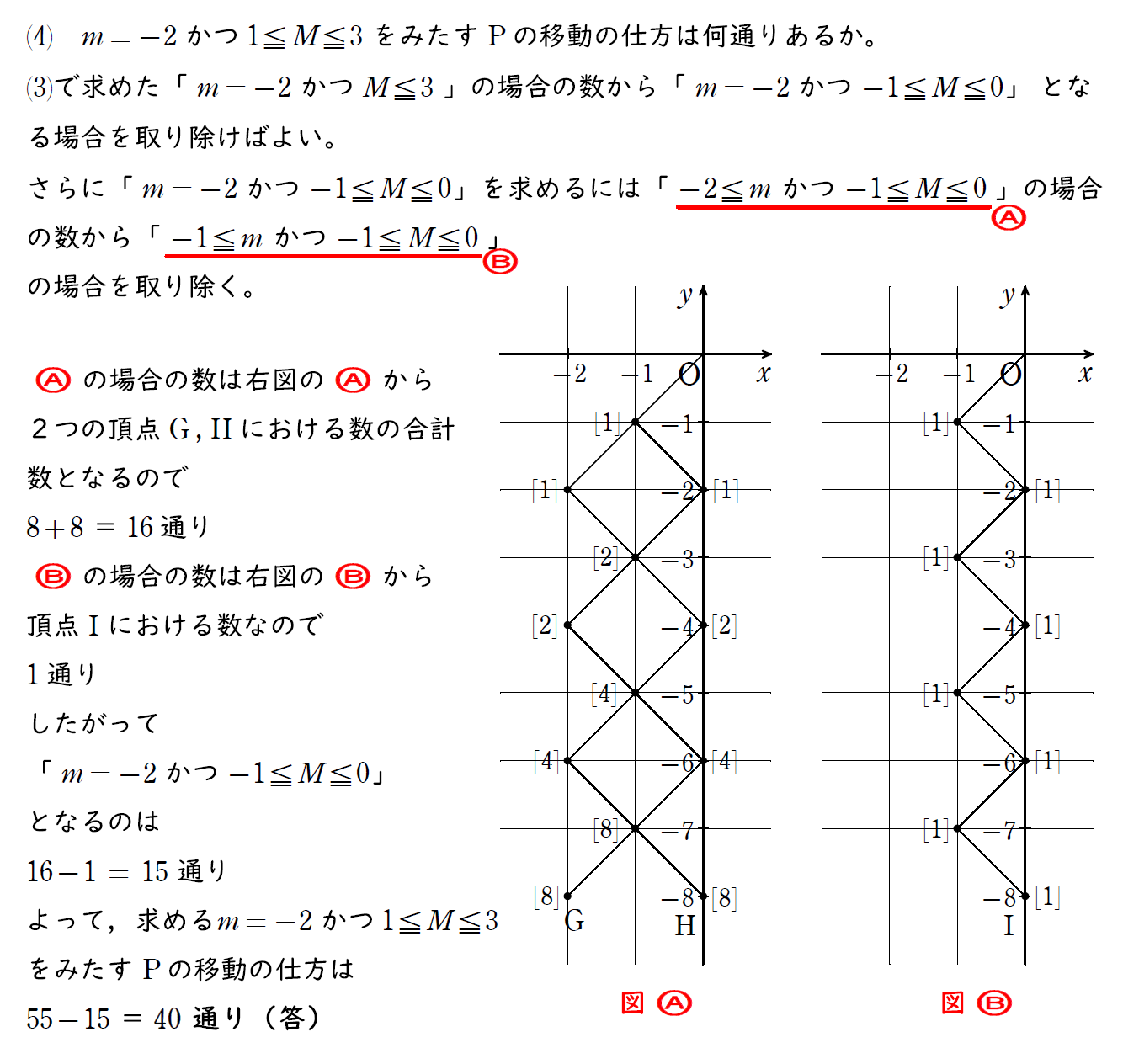
終わりに
確率ではなく場合の数もこの問題のように出題されることも多く、コンビネーションやパーミテーションなどの公式を使うことなく、一つ一つ丁寧に数え上げることが大切だ。
これを意識して普段から数え上げをミスすることなくしっかり答が合うまで練習しておこう。









コメント