参考書や予備校のサイトを利用して大学入試問題を勉強している人の中で「解説を読んでも理解できない」と思ったことはありませんか?
YouTubeなどに解説動画がありますが「通信環境がない」とか「動画を見るのはめんどう」思う人も多いでしょう。
この記事では読むだけで動画よりもわかりやすくどの参考書よりも細かく解説をしていきます。
2023九州大大問4(文系)
問題

複素数と数列の融合問題。
複素数の分野では ω(オメガ)の性質を用いた内容。
教科書ではあまり取り上げていないが、受験数学では必須の内容なのでしっかり練習しておきたい。
漸化式は2項間漸化式と連立漸化式を使う。
解説
(1) の解説
1の3乗根、いわゆるω問題。
オメガの性質は次の2つをおさえておこう。
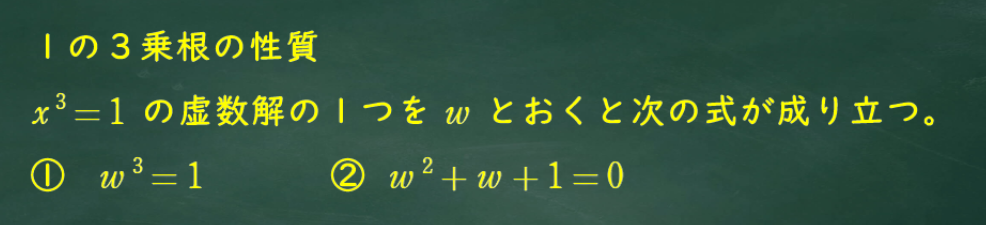

(2) の解説
いわゆる確率漸化式の問題。
問題文で与えられた条件から2項間漸化式を作る。

(3) の解説
まずは ω の性質を用いて共役な複素数の計算をしておく。(1) が誘導になっている。

問題文にあるさいころの出目による zk と zk+1 の関係式を一つ一つ丁寧に調べていけば、それぞれの確率を求めることができる。

最後にもうひとパターン。
この問題は (4) のことも考えて解答を作ることもできるが、とりあえず (3) を解くことだけを考えた解答を紹介する。

(4) の解説
これも(3)同様、問題文の条件から一つ一つ丁寧にたどっていけばそれぞれの確率を求められる。
zn は 0、1、ω、ω2 のいずれかとなるのでそれぞれの確率を設定し、4つの連立漸化式を解くことになる。

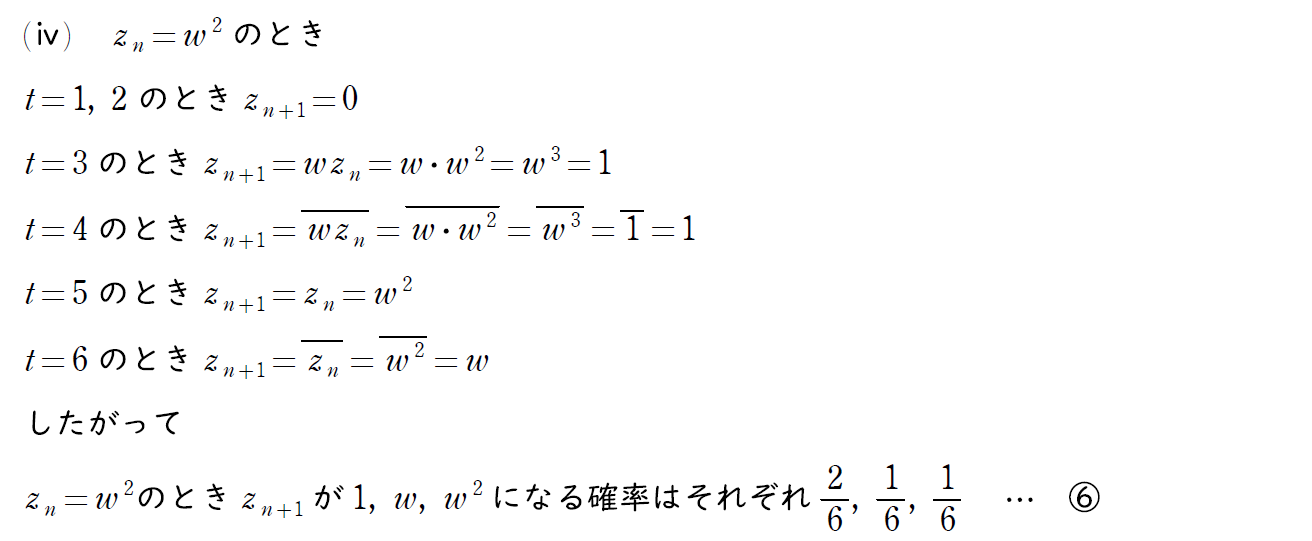
4つそれぞれの確率が求まったら、連立漸化式を立てる。
最後にそれらを連立するときに ⑩ , ⑪ の条件を立てることを忘れずに。

終わりに
確率の試行自体は複雑ではないが、確率漸化式に慣れていないと立式するのが難しいかもしれない。
それに加えて複素数の問題との融合なので慣れていない生徒は手を付けることができなかった者も多いだろう。
確率漸化式は文系、理系問わず頻出の分野なので演習をしっかり行っておこう。







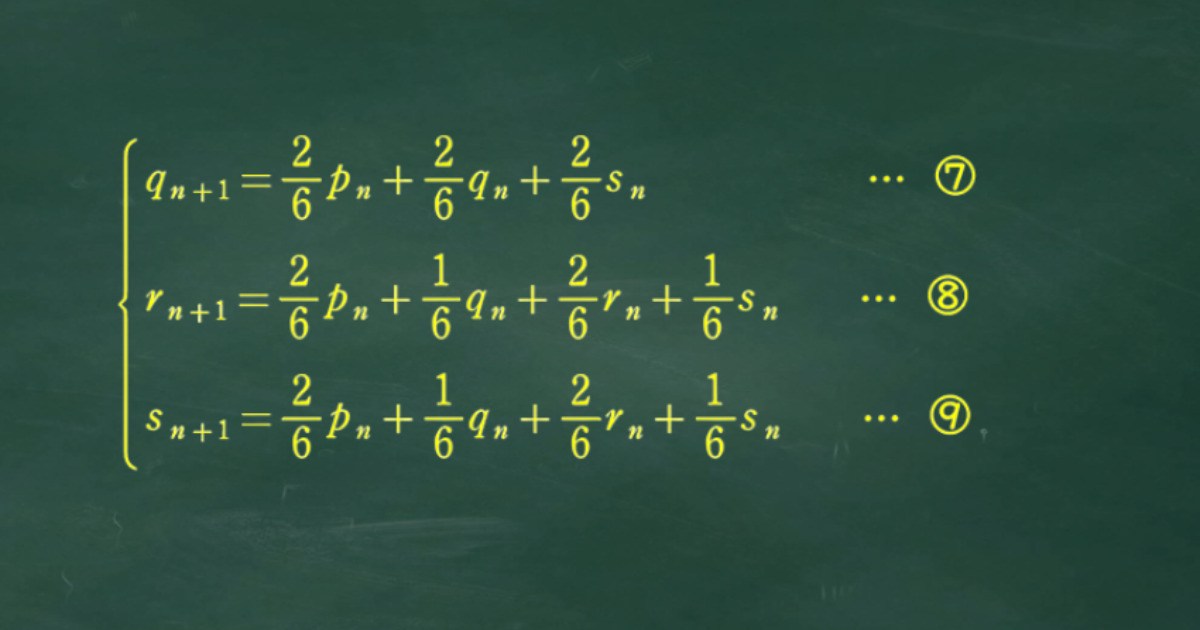


コメント